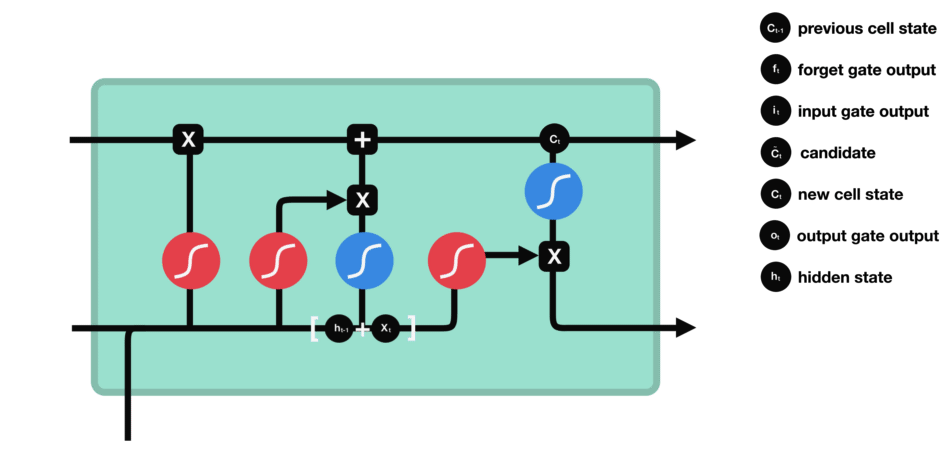
LSTM

Long ShortTerm 网络，一般就叫做LSTM，是一种RNN特殊的类型，可以学习长期依赖信息。当然，LSTM和基线RNN并没有特别大的结构不同，但是它们用了不同的函数来计算隐状态。

LSTM的"记忆"我们叫做细胞/cells，你可以直接把它们想做黑盒，这个黑盒的输入为前状态 h~t-1~ 和当前输入 x~t~ 。这些"细胞"会决定哪些之前的信息和状态需要保留/记住，而哪些要被抹去。实际的应用中发现，这种方式可以有效地保存很长时间之前的关联信息。

什么是LSTM网络

简介

::: tip 例子

  • 当你想在网上购买生活用品时，一般都会查看一下此前已购买该商品用户的评价。
  • 当你浏览评论时，你的大脑下意识地只会记住重要的关键词，比如"amazing"和"awsome"这样的词汇，而不太会关心"this"、"give"、"all"、"should"等字样。如果朋友第二天问你用户评价都说了什么，那你可能不会一字不漏地记住它，而是会说出但大脑里记得的主要观点，比如"下次肯定还会来买"，那其他一些无关紧要的内容自然会从记忆中逐渐消失。 ::: 而这基本上就像是 LSTM 或 GRU 所做的那样，它们可以学习只保留相关信息来进行预测，并忘记不相关的数据。简单说，因记忆能力有限，记住重要的，忘记无关紧要的。

提出与改进

LSTM由Hochreiter&Schmidhuber(1997)提出，并在近期被AlexGraves进行了改良和推广。在很多问题，LSTM都取得相当巨大的成功，并得到了广泛的使用。 LSTM通过刻意的设计来避免长期依赖问题。记住长期的信息在实践中是LSTM的默认行为，而非需要付出很大代价才能获得的能力！

网络结构

RNN结构

所有RNN都具有一种重复神经网络模块的链式的形式。在标准的RNN中，这个重复的模块只有一个非常简单的结构，例如一个tanh层。 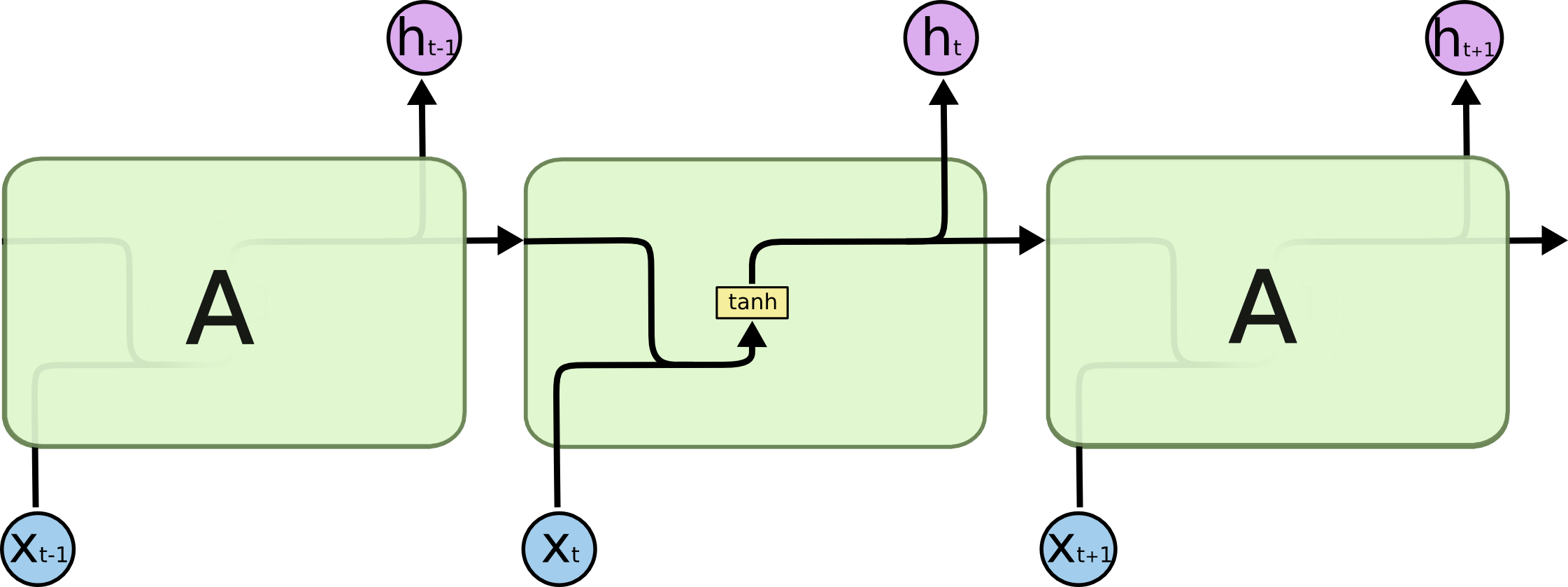Img 激活函数Tanh 作用在于帮助调节流经网络的值，使得数值始终限制在 -1 和 1 之间。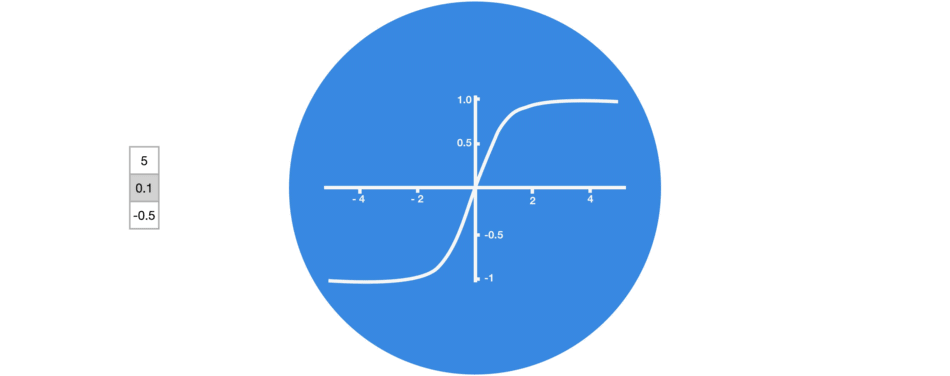 Img

LSTM结构

LSTM同样是这样的结构，但是重复的模块拥有一个不同的结构。具体来说，RNN是重复单一的神经网络层，LSTM中的重复模块则包含四个交互的层，三个Sigmoid 和一个tanh层，并以一种非常特殊的方式进行交互。 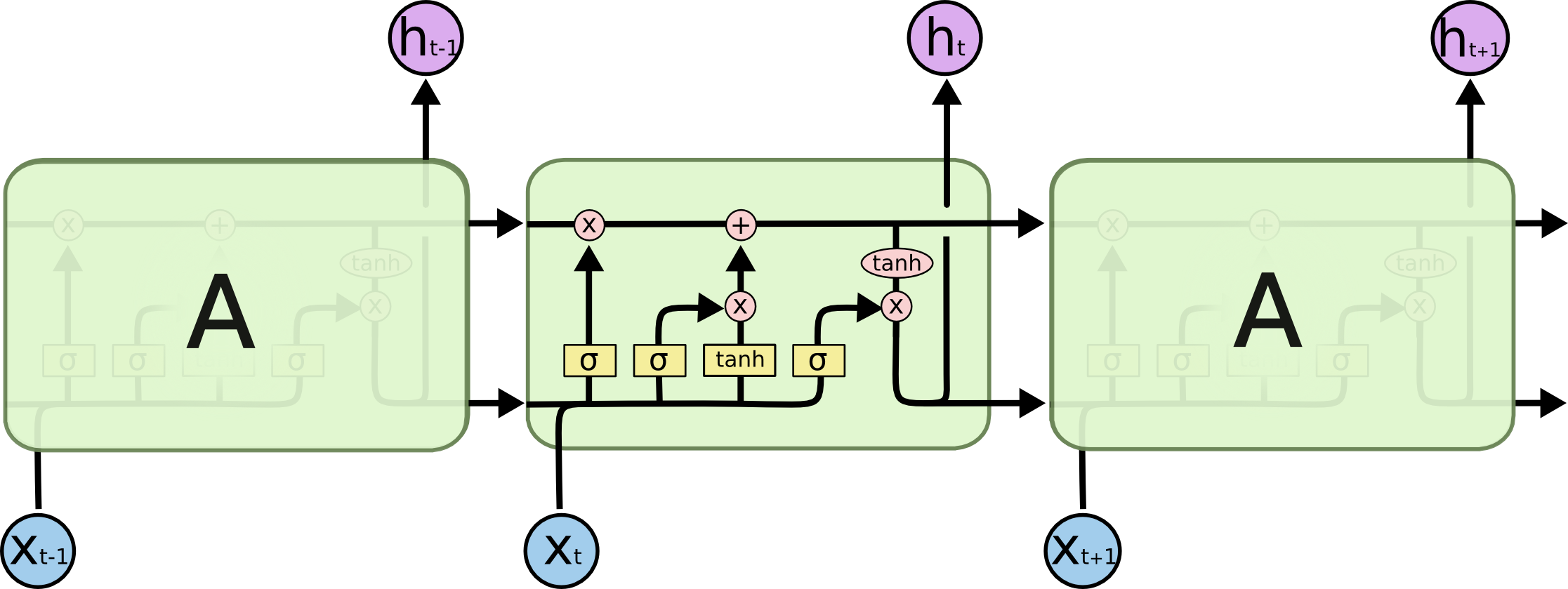Img 上图中，σ表示的Sigmoid 激活函数与 tanh 函数类似，不同之处在于 sigmoid 是把值压缩到0~1 之间而不是 -1~1 之间。这样的设置有助于更新或忘记信息： ::: tip Sigmoid函数σ

  • 因为任何数乘以 0 都得 0，这部分信息就会剔除掉；
  • 同样的，任何数乘以 1 都得到它本身，这部分信息就会完美地保存下来。 Img ::: 相当于要么是1则记住，要么是0则忘掉，所以还是这个原则：因记忆能力有限，记住重要的，忘记无关紧要的。
图标 含义
Img 学习到的神经网络层
Img Pointwise操作
Img 传输着一整个向量，从一个节点的输出到其他节点的输入
Img 合在一起的线表示向量的连接
Img 分开的线表示内容被复制，然后分发到不同的位置。

LSTM的核心思想

细胞

LSTM的关键就是细胞状态，水平线在图上方贯穿运行。 细胞状态类似于传送带。直接在整个链上运行，只有一些少量的线性交互。信息在上面流传保持不变会很容易。 Img LSTM有通过精心设计的称作为"门"的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个sigmoid神经网络层和一个pointwise乘法的非线性操作。

如此，0代表"不许任何量通过"，1就指"允许任意量通过"！从而使得网络就能了解哪些数据是需要遗忘，哪些数据是需要保存。 Img

LSTM拥有三种类型的门结构：遗忘门、输入门和输出门，来保护和控制细胞状态。下面，我们来介绍这三个门。

逐步理解LSTM

步骤 含义
遗忘门 决定我们会从细胞状态中丢弃什么信息
输入门 确定什么样的新信息被存放在细胞状态中
输出门 确定输出什么值

遗忘门

流程

在我们LSTM中的第一步是决定我们会从细胞状态中丢弃什么信息。这个决定通过一个称为"遗忘门"的结构完成。 ::: tip 遗忘门流程

  • 读取上一个输出h~t-1~和当前输入x~t~，做一个Sigmoid 的非线性映射
  • 然后输出一个向量f~t~（该向量每一个维度的值都在0到1之间，1表示完全保留，0表示完全舍弃，相当于记住了重要的，忘记了无关紧要的）
  • 最后与细胞状态C~t-1~相乘。 ::: 类比到语言模型的例子中，则是 ::: tip 例子 基于已经看到的预测下一个词。在这个问题中，细胞状态可能包含当前主语的性别，因此正确的代词可以被选择出来。当我们看到新的主语，我们希望忘记旧的主语，进而决定丢弃信息。 :::

    公式理解

\(f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\) 大部分初学的读者看到这，可能会有所懵逼，没关系，我们分以下两个步骤理解：

对于上图右侧公式中的权值W~f~，准确的说其实是不共享，即是不一样的。有的同学可能第一反应是what？别急，我展开下你可能就瞬间清晰了，即： \(f_{t}=\sigma\left(W_{f h} h_{t-1}+W_{f x} x_{t}+b_{f}\right)\)

| 图标 | 含义 | | – | – | |红圈|Sigmoid激活函数| |篮圈|tanh函数| 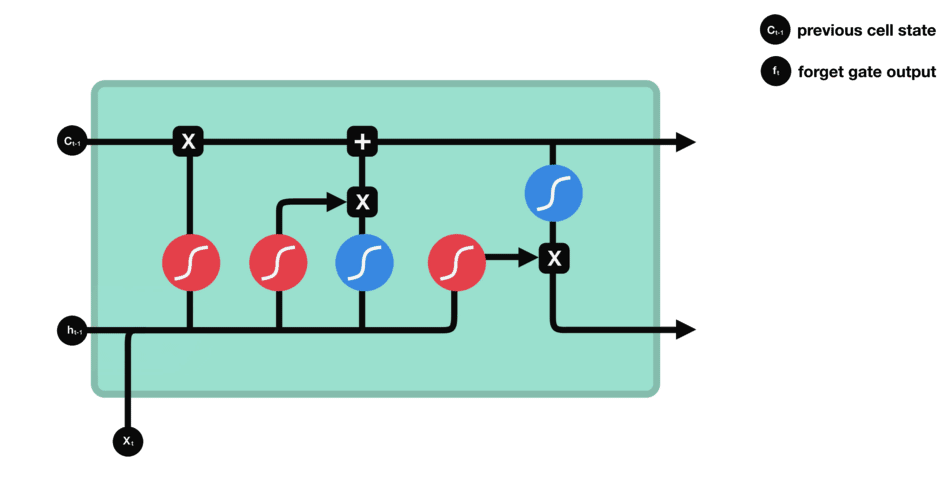Img

输入门

流程

下一步是确定什么样的新信息被存放在细胞状态中。这里包含两个部分： ::: tip 流程

  • sigmoid层称"输入门层"决定什么值我们将要更新；
  • 一个tanh层创建一个新的候选值向量$\tilde{C}_{t}$，会被加入到状态中。 ::: 在我们语言模型的例子中， ::: tip 例子 我们希望增加新的主语的性别到细胞状态中，来替代旧的需要忘记的主语，进而确定更新的信息。 :::

    公式理解

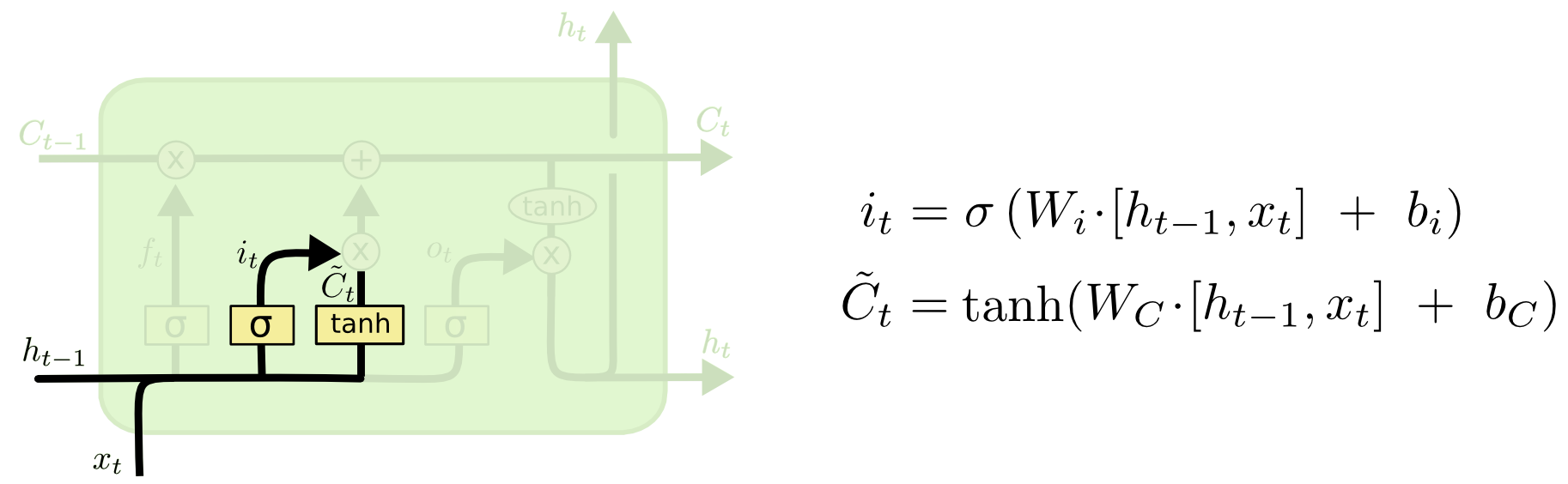    Img 继续分两个步骤来理解：

首先，为便于理解图中右侧的两个公式，我们展开下计算过程，即 \(i_{t}=\sigma\left(W_{i h} h_{t-1}+W_{i x} x_{t}+b_{i}\right)\) \(\tilde{C}_{t}=\tanh \left(W_{C h} h_{t-1}+W_{C x} x_{t}+b_{C}\right)\) 其次，上图！ Img

状态更新

现在是更新旧细胞状态的时间了，${C}{t-1}$更新为${C}{t}$。 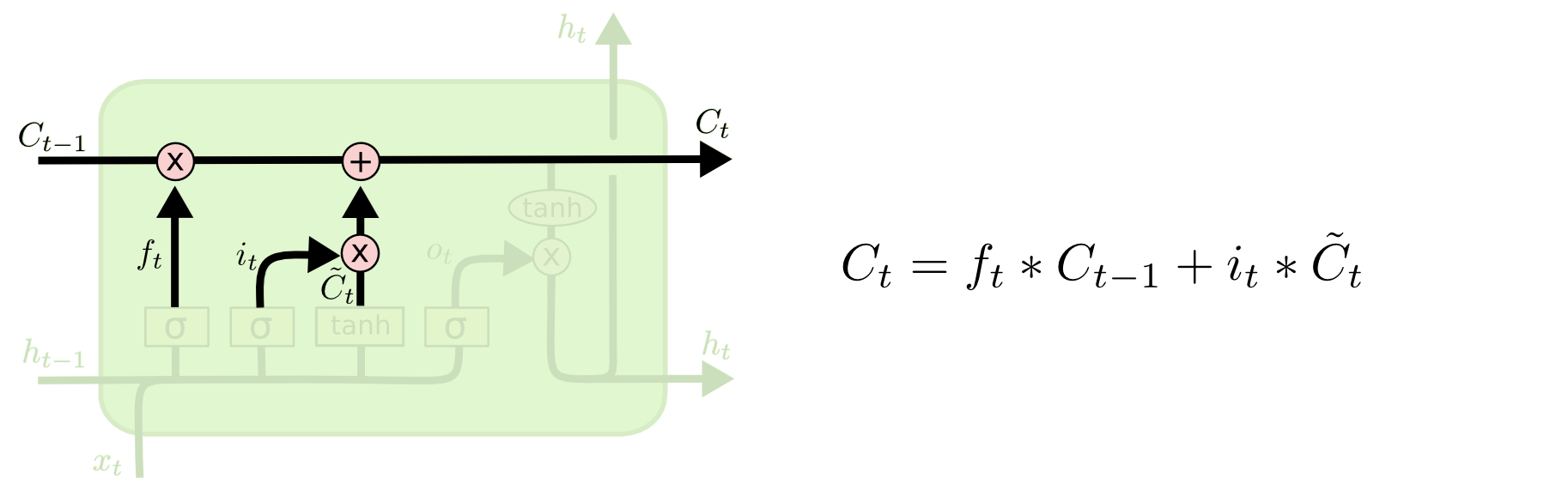Img

前面的步骤已经决定了将会做什么，我们现在就是实际去完成。

  • 把旧状态与$f_t$相乘，丢弃掉我们确定需要丢弃的信息。
  • 接着加上$i_t*\tilde{C}_{t}$。

这就是新的候选值，根据我们决定更新每个状态的程度进行变化，类似更新细胞状态。 在语言模型的例子中， ::: tip 例子 这就是我们实际根据前面确定的目标，丢弃旧代词的性别信息并添加新的信息的地方。 ::: 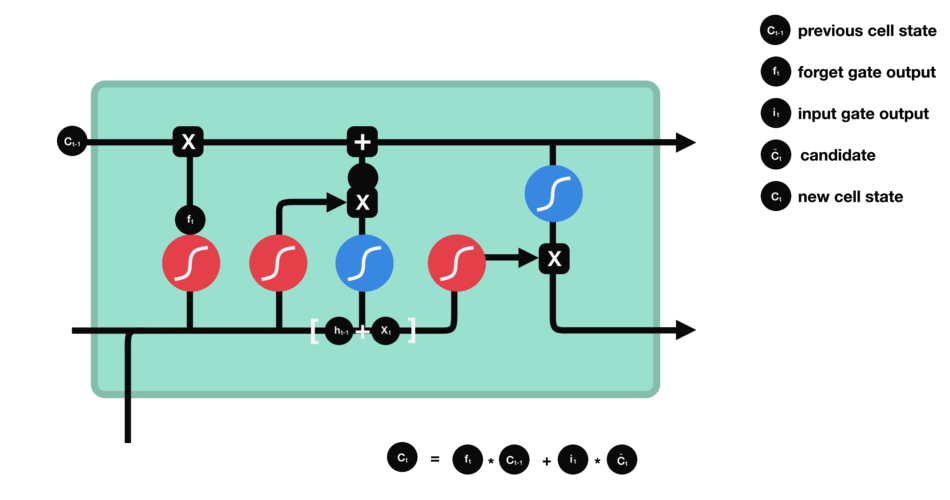Img

输出门

最终，我们需要确定输出什么值。这个输出将会基于我们的细胞状态，但是也是一个过滤后的版本。 ::: tip 流程 首先，我们运行一个sigmoid层来确定细胞状态的哪个部分将输出出去。 接着，我们把细胞状态通过tanh进行处理（得到一个在-1到1之间的值）并将它和sigmoid门的输出相乘，最终我们仅仅会输出我们确定输出的那部分。 ::: 在语言模型的例子中， ::: tip 例子 因为他就看到了一个代词，可能需要输出与一个动词相关的信息。例如，可能输出是否代词是单数还是负数，这样如果是动词的话，我们也知道动词需要进行的词形变化，进而输出信息。 :::

公式理解

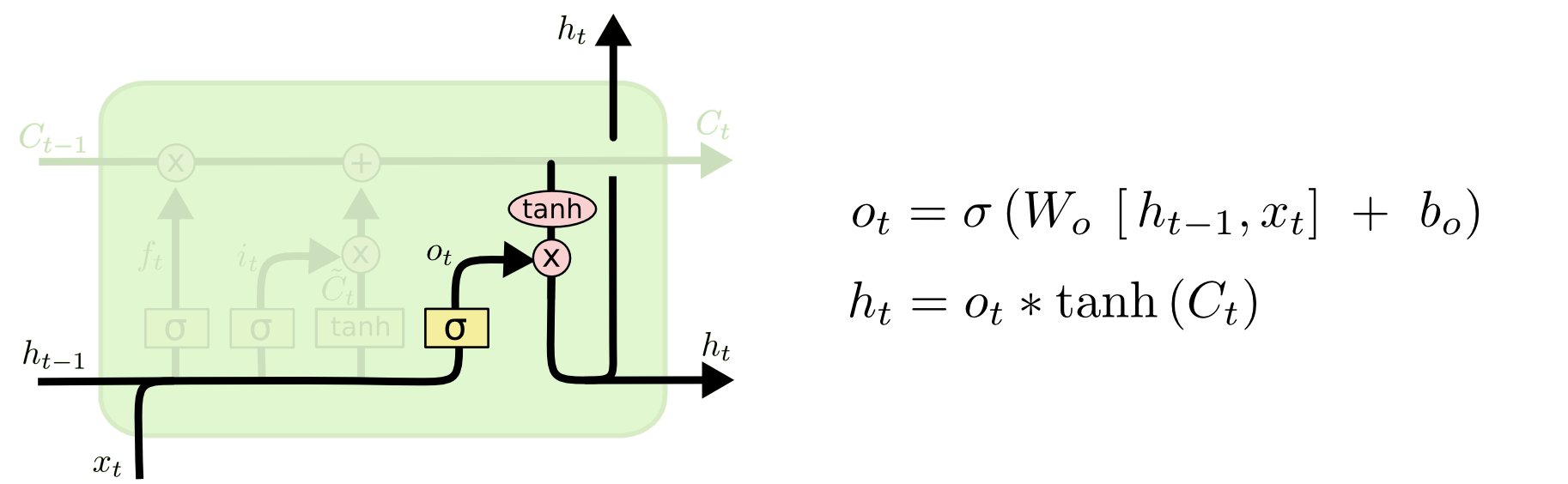Img 依然分两个步骤来理解：

展开图中右侧第一个公式，$o_{t} = \sigma (W_{oh}h_{t-1} + W_{ox}x_{t} + b_{o})$ 最后一个动图： Img