卷积神经网络DeepConvNet
解决问题
- 卷积神经网络
设计选择对解码准确性有什么影响? - 卷积神经网络
训练策略对解码准确性有什么影响?成果
端到端训练的深度卷积网络解码EEG任务相关信息的
准确度至少与FBCSP相同。 -
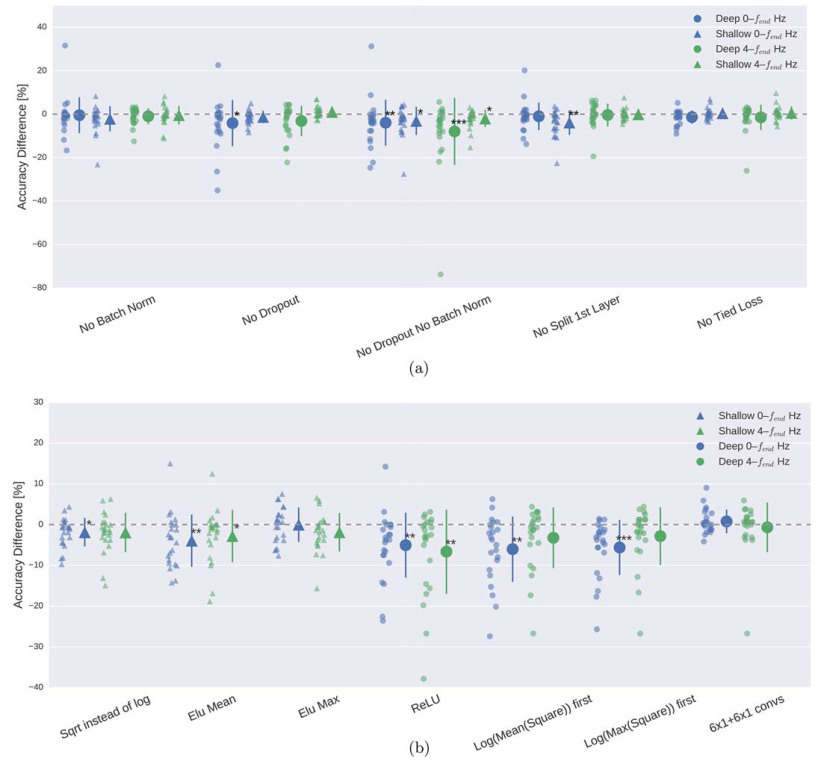
评估了脑电解码任务中大量的卷积网设计选择,并表明最近从深度学习领域发展的方法,如归一化和指数线性单元是达到高解码精度的关键。
-
证明了裁剪训练可以提高深度卷积神经网络的解码精度,并描述了一种计算效率高的训练策略,以每次脑电图试验在更大数量的输入作物上训练卷积神经网络。
- 开发和应用新颖的可视化图像,高度表明深度卷积网络学会使用与(alpha, beta和gamma)相关的频带功率,具有有意义的空间分布。
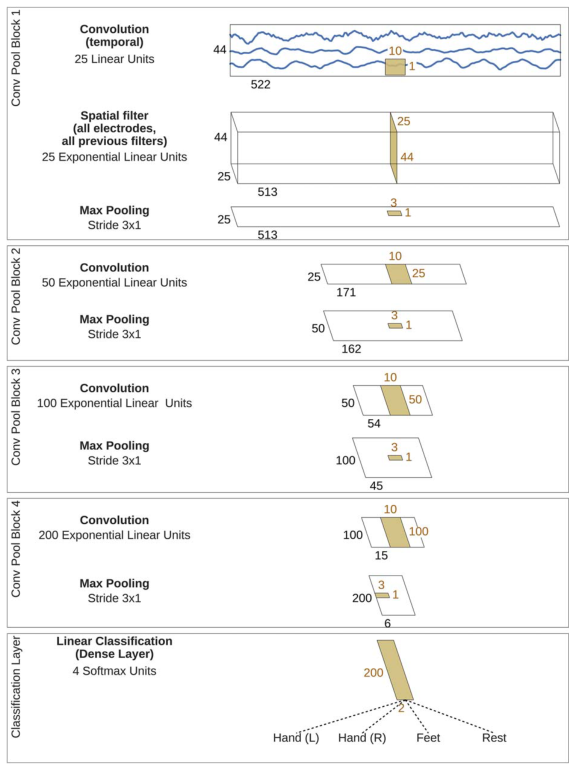
深度卷积网络有4个卷积-max-pooling块,其中一个特殊的第一个块设计用于处理EEG输入,然后是3个标准的卷积-max-pooling块和一个密集的softmax分类层。
第一个卷积块被分为两层——每个电极一个输入通道,而rgb图像有三个输入通道(每个颜色一个)。在第一层中,每个滤波器随时间进行卷积。
在第二层中,每个滤波器对所有可能的电极对使用前一时间卷积的滤波器进行加权的空间滤波。请注意,由于在这两层之间没有激活函数,它们原则上可以合并为一层。然而,通过强制将线性变换分离为时间卷积和空间滤波器的组合,使用两层隐含地正则化了整体卷积。
Deep ConvNet
Shallow ConvNet
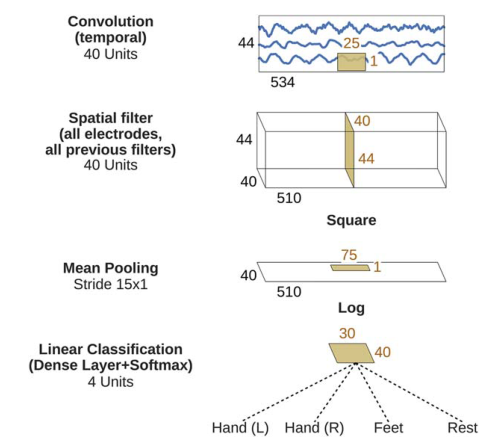
训练
Dropout=0.5
损失函数
\(p\left(l_{k} \mid f\left(X^{j} ; \theta\right)\right)=\frac{\exp \left(f_{k}\left(X^{j} ; \theta\right)\right)}{\sum_{m=1}^{K} \exp \left(f_{m}\left(X^{j} ; \theta\right)\right)}\) \(\theta^{*}=\arg \min _{\theta} \sum_{j=1}^{N} \operatorname{loss}\left(y^{j}, p\left(l_{k} \mid f_{k}\left(X^{j} ; \theta\right)\right)\right)\) 
其中h为函数参数,E为电极个数,T为时间步数,K为可能的输出标签个数。 作为训练卷积网络的常见方法,参数通过使用反向传播计算的解析梯度通过随机梯度下降进行优化
结果
达到了与广泛使用的滤波器组公共空间模式(FBCSP)算法(平均解码精度为82.1% FBCSP,深度ConvNets为84.0%)相同的性能。同时计算了扰动试验的准确性。对于所有受试者的训练集的所有扰动,准确率保持在未扰动数据的99.5%以上。 
 几乎所有受试者在4-fend-Hz频率范围内的深度卷积网具有更好的准确性。
几乎所有受试者在4-fend-Hz频率范围内的深度卷积网具有更好的准确性。 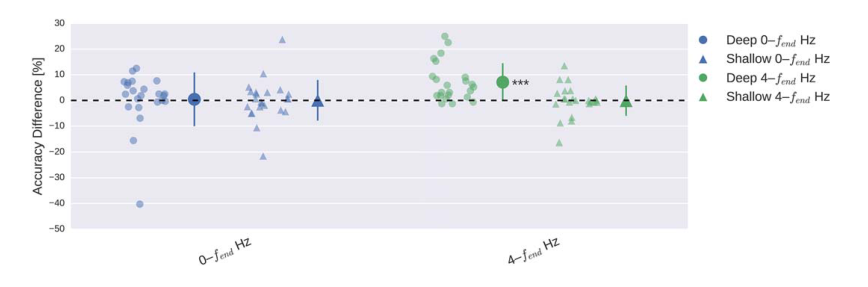
代码结果
DeepConvNet
100轮训练结果 

ShallowFBCSPNet
100轮训练结果 


EEGNet
100轮训练结果 
 300轮训练结果
300轮训练结果 

