脑电图中人眼伪影的去除—结合DWT和ANC的便携式改进方法
干扰
头皮电位振幅一般为20 ~ 100 μV。不幸的是,记录的数据会受到非脑电位干扰的污染,如肌肉活动或基线漂移的肌电图和电源线干扰(50/60 Hz)等。在EEG采集过程中,眼球运动和眨眼的污染也会造成记录数据的严重失真。这两种环境因素都会在眼睛周围产生巨大的电势,称为眼伪物(OAs)。眨眼产生的信号振幅是环境脑电图信号的十倍以上。在脑电图采集过程中,即使受试者被要求闭上眼睛,也会记录他们的眼球运动。
方法
本文采用了一种基于==小波变换==和==自适应噪声抵消ANC==的新模型去噪。我们的新方法的第一步和最重要的一步是使用DWT构造参考信号。以该参考信号为基础,建立了基于自适应控制的新模型;因此,采用DWT和ANC相结合的方法。在脑电图信号中,电磁感应常用于去除电力线干扰。
污染表示
记录的脑电图信号受到OAs的污染,这种污染被认为是脑电图信号中的一种附加噪声。因此,我们可以写出以下表达式:  | 名称 | 说明 | | – | – | |
| 名称 | 说明 | | – | – | | EEGrec(t) | 记录脑电图信号 | | EEGtrue(t) | 脑皮层活动与不受干扰的脑电图信号 | | k·OAs(t) | 眼球运动引起的oa |
通过有效地去除k·OAs(t),可以从EEGrec(t)中得到EEGtrue(t)。
在我们的模型中,后一个操作包括两个主要步骤。
首先是参考信号的构造;二是基于递归最小二乘(RLS)算法,应用自适应校正(ANC)去除记录的脑电信号中的oa。
频谱分析主要集中在低频波段,因此采用DWT在频域构造频谱分析。
DWT是信号和图像的多分辨率表示。
它可以将信号分解为多尺度表示。它是一种常用的分析非平稳信号的工具
小波
小波在小波变换中可以有效地从时变不稳定的脑电信号中构建时域和频域信息。与傅里叶变换不同,小波变换可以使用各种不同性质的基函数。
自适应滤波器
另一种估计加性噪声干扰的方法是使用自适应滤波器。在ANC滤波器中,当自动调整系数以达到最优滤波时,干扰源作为参考。
自适应滤波器的核心是自适应算法。有几种选择:最常见的算法是最小均方(LMS)和最小均方(RLS)。当环境噪声为平稳随机信号时,基于LMS算法的自适应系统具有较好的性能。然而,当环境噪声不稳定时,随着噪声统计特性的变化,LMS算法难以自适应跟踪噪声。相比之下,RLS算法在非平稳环境中具有良好的性能,能够跟踪缓慢变化的参数。因此,本研究采用一种基于RLS算法的自适应控制算法来去除脑电信号中的OAs。该滤波器根据加权平方误差和最小标准差调整其系数,得到最优滤波器系数。
ANC的主输入dj = sj + n0,其中dj为损坏信号,n0为要偏移的噪声,与sj不相关。参考输入xj = n1, n1为与n0相关,与sj不相关的噪声信号,yj为自适应滤波器的输出。系统从一次输入减去yj得到zj, zj为系统输出,即估计信号为zj = dj−yj。RLS算法概述如下:
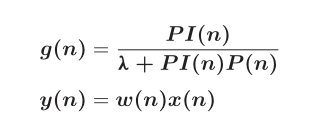
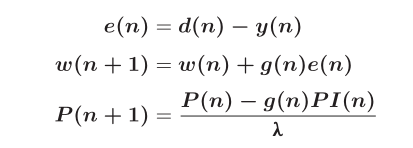 | 名称 | 说明 | | – | – | |
| 名称 | 说明 | | – | – | | PI(n) | 互相关联矩阵 PI(n)=x(n)P(n) P(0)= δI| | δ | 一个足够大的正数 | | g(n) | 增益向量 | | w(n) | 自适应滤波器的加权向量 | | g(n) | 增益向量 |
方案
1)对污染脑电信号进行小波分解,得到小波系数。有几种可能的母小波函数,但经过多次测试,我们发现Daubechies 4族在形态学上与OAs更为相似。
因此,我们选择Daubechies 4小波作为母小波函数。如果小波分解的电平太小,很难有效地去除噪声;但如果分解等级太高,信噪比就会较差。因此,我们选择了七个分解层作为折衷方案。
2)根据最小的风险值,选择软阈值,将其应用到三个最低级别系数上,得到这三个级别的新系数。
阈值的选择可以与硬阈值或软阈值相关。采用软阈值可以使小波系数按照一个固定的向量收缩为零,并且软阈值所得到的小波系数具有良好的连续性和易于处理。 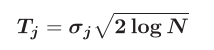 | 名称 | 说明 | | – | – | |
| 名称 | 说明 | | – | – | | j | 分解能级 | | N | 样本个数 | | Tj | 阈值 | | 0.6745 | 中位数绝对值估计 | | σj | 噪声信号标准差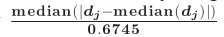 |
|
3)对新的小波系数进行小波重构,构建参考信号。
4)以构造的参考信号为输入,对受污染脑电信号进行ANC处理,去除OAs。
虽然一些研究人员使用DWT构建OA参考信号,但我们提出的方法与他们的方法存在差异。以往的研究都是将阈值应用在每一层的系数上,而本文将阈值应用在最低的三个系数上,因为oa主要包含在这三个层中,从而减少了计算开销。图2显示了一个受污染的脑电图信号和使用我们的模型构造的参考信号。
误差评估工具:MSE,MAE
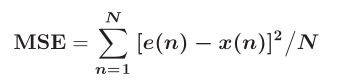

平均绝对误差 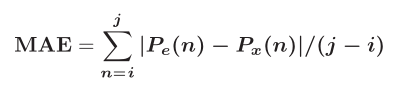 另一个验证噪声数据和去噪数据的性能指标是频域的相关性。两个信号x和y之间的频率相关性可以用公式来计算:
另一个验证噪声数据和去噪数据的性能指标是频域的相关性。两个信号x和y之间的频率相关性可以用公式来计算: 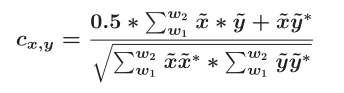
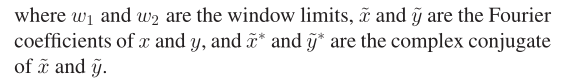
其中w1和w2是窗口限制,x和y是x和y的傅里叶系数,并且ndx∗和ndy∗是ndx和ndy的复合共轭。
结果
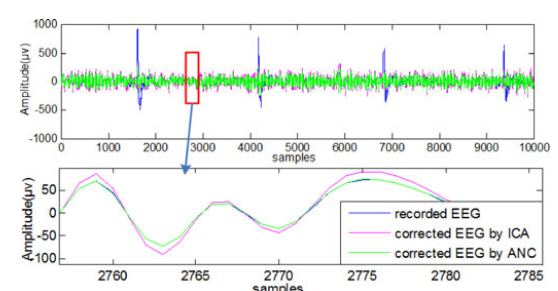
与传统方法相比,自适应滤波方法具有以下优点:
1)从原始单通道脑电信号中提取参考信号简单、计算效率高,同时避免了同步采集人眼参考信号。因此,该设计促进了轻便便携设备的使用。
2)根据眼球运动和眨眼动态调整ANC滤波器的系数,可以在保留真实脑电图信息的同时有效地去除oa。由于ANC滤波器是基于RLS算法自适应调整系数,因此比静态系数滤波器具有更大的灵活性。
3)信号跟踪性能良好。该滤波器不会破坏没有OAs的干净脑电区域,因此能很好地保存脑电记录的固有成分。