卷积神经网络EEGNet

简介

EEG的分析中，传统方法涉及到两个部分：特征提取和分类。对于不同范式下的EEG，往往需要设计不同的特征，例如：

  • 情绪分类中使用功率谱或微分熵特征
  • 运动想象分类中往往使用频域和空域特征。

那么是不是可以设计一个模型可以用于不同的范式呢？EEGNet的出现一定程度上回答了这个问题——或许可以。实验的结果表示了EEGNet在不同范式下的分类任务，均可以得到有竞争力的结果，同时在被试内和跨被试的分类中也取得了较好的结果，具有较好的鲁棒性。

思路

利用深度卷积和可分离卷积构造一个单一的CNN架构来准确地分类来自不同BCI范式的脑电信号，同时尽可能地紧凑（compact，模型中的参数数量）。

摘要

介绍了脑电特征提取模型的方法，该模型封装了脑机接口的脑电特征提取概念。在实验部分，将EEGNet和在受试者内和跨受试者分类方面与目前最先进的方法进行对比，包括四种BCI范式：

  • P300视觉诱发电位
  • 错误相关负性反应
  • 运动相关皮层电位
  • 感觉运动节律 补充

在训练数据有限的情况下，EEGNet算法比参考算法具有更好的泛化能力和较高的性能。我们还证明了EEGNet对ERP和基于振荡的BCIs都有很好的泛化。此外，我们还演示了三种不同的方法来可视化经过训练的EEGNet模型的内容，从而能够解释学习到的特征。

创新

  • 可以应用于多种不同的BCI范式
  • 可以用非常有限的数据进行训练
  • 可以产生神经生理学上可解释的特征

结构

框图

Img

符号说明

|符号|说明| |:–:|:–:| | C | 导联数（64） | | T | 时间点数（128） | | F1 | 时间滤波器数 | | D | 深度乘法器(空间滤波器数) | | F2 | 点态滤波器数 | | N | 类数 | | p{rowspan=2} | p = 0.5表示主题内分类| || p = 0.25表示交叉主题分类| —

第一部分

::: tip 在Block 1中，按顺序执行两个卷积步骤 :::

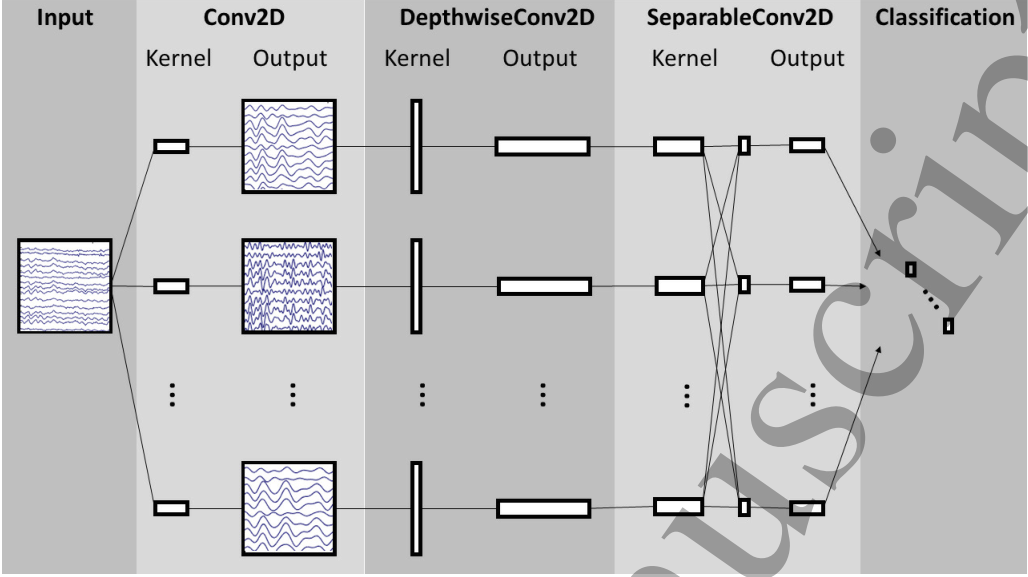
结构图

Img

Conv2D

F1个滤波器，卷积核大小为（1，64）2D卷积，卷积核长度为数据采样率的一半（这里是128Hz/2=64），输出F1个包含不同带通频率下脑电图信号的特征图（feature map）。

BatchNorm

将时序卷积核的长度设置为采样率的一半，可以捕获2Hz及以上的频率信息。补充

DepthwiseConv2D

然后，使用大小为（C，1）的深度卷积（Depthwise Convolution）来学习空间滤波器。因为深度卷积并没有全连接到以前的所有特征图，因此，减少了可训练参数的数量。同时，这种操作提供了一种为每个时序滤波器学习其空间滤波器的直接方法，从而能够有效地提取频率特定的空间滤波器。参数D控制每个特征图要学习的空间滤波器的数量（图中显示了D=1）。 补充

这种两步卷积序列的部分灵感来自于滤波器组公共空间模式（FBCSP）算法，本质上类似于另一种分解技术，即双线性判别成分分析。

Activation

对应两个卷积未使用非线性激活函数，是由于在使用非线性激活时性能没有显著提高。之后，沿着特征图维度应用批量归一化，应用指数线性单元（ELU），使用Dropout技术。（受试者内分类：DropOut概率为0.5；跨被试分类：DropOut概率为0.25）。 \(\operatorname{ELU}(a)=x ,x>0\) \(\operatorname{ELU}(a)=e^{x}-1 ,x<0\) \(\operatorname{RELU}(a)=\max (0, a)\) 补充

Pool

采用一个平均大小为（1，4）的池化层，将信号的采样率降低到32Hz。

Dropout

我们还通过对每个空间滤波器的权值使用1的最大范数约束对其进行正则化；

第二部分

::: tip Block 2,使用可分离卷积:深度+点式 :::

结构图

Img

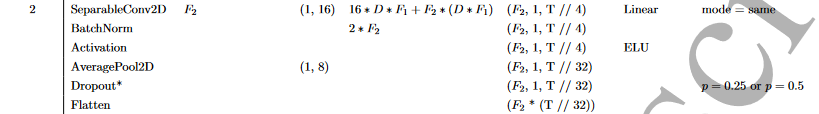
SeparableConv2D

在Block 2中，使用可分离卷积（Separable Convolution），即深度卷积（表中核大小为（1，16），表示32Hz时500毫秒的脑电图活动），然后是F2个（1，1）点式卷积（Pointwise Convolutions）。 补充

可分离卷积的主要优点是： （1）减少了特征映射的参数个数； （2）通过先学习一个单独"综合"每个特征图的（1，1）的核，然后优化合并输出，显式地解耦特征图内（Depthwise）和特征图间（Pointwise）的关系。

Activation

对于EEG，Separable Convolution将学习如何在时间维度（depthwise convolution）"综合"各特征图的核以及如何优化组合（Pointwise Convolution）分开，这一操作对于EEG信号十分有用，因为不同的特征图代表了数据在不同时间尺度上的信息。 在本例中，我们首先学习每个特征映射的500毫秒"综合"，然后结合输出。

Pool

此后，大小为（1，8）的平均池层用于降维。

Dropout

在分类的Block中，特征直接传递给N类的softmax输出，以减少模型中自由参数的数量。

Flatten

展平给全连接层

模型训练

使用Adam优化器建立模型，最小化分类交叉熵损失函数。运行500个训练迭代（epoch）并执行验证停止，选择最低验证集损失的模型。

结果

对比方法

  • 基于CNN的DeepConvNet
  • 基于CNN的ShallowConvNet
  • 基于空间滤波和黎曼几何分类器的XDAWN+RG

参数数量

Img

对于所有基于cnn的模型，每个模型和每个数据集的可训练参数的数量。我们发现，在所有数据集上，EEGNet模型比DeepConvNet和ShallowConvNet模型都要小两个数量级。

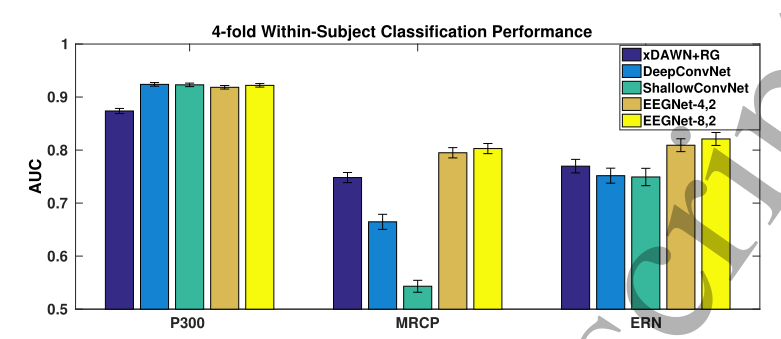
被试内分类

Img P300、ERN和MRCP数据集：4折被试内分类平均性能；对于P300数据集，基于CNN方法性能差异非常小，但在MRCP数据集中存在显著的差异（EEGNet显著优于其他模型）；对于ERN数据集，EEGNet模型的性能同样显著优于其他方法。 Img SMR数据集：4折平均分类性能；DeepConvNet显著低于其他模型p < 0.05, ShallowConvNet和EEGNet-8,2的性能与FBCSP相似。

跨被试分类

Img P300、ERN和MRCP数据集：跨被试分类性能；P300和MRCP数据集上DeepConvNet和EEGNet模型的性能差异最小，同时都高于ShallowConvNet；ERN数据集上，参考的xDAWN+RG方法高于其他所有模型。 Img SMR数据集：跨被试平均分类性能；所有基于CNN的模型性能相似，同时略微高于FBCSP。

代码实现部分

数据集

训练集：0 - 144 = 144 验证集：144 - 216 = 72 测试集：216 - 288 = 72

功率谱密度

Img

结果

Img Img Img

补充

四种BCI范式

| |名称|描述|处理| |–|–|–|–| |P300|视觉诱发电位|可以由视觉刺激引起|FIR滤波器进行1-40Hz数字带通滤波，下采样到128 Hz。在刺激开始后0-1s提取目标和非目标| |ERN|错误相关负性电位||使用FIR滤波器实现1-40Hz滤波，并下采样到128Hz。在反馈后0-1.25s提取正确和错误反馈的EEG信号| |MRCP|运动相关皮层电位|可以由手脚运动引起|使用FIR滤波器实现1-40Hz滤波，并下采样到128Hz。在反馈后0.5-1s提取左右手两分类的EEG信号| |SMR|感觉运动节律||在0.5-2.5秒使用4-40Hz三阶巴特沃斯滤波器对数据进行过滤| 返回

BatchNorm简述

Batch-Normalization (BN)是一种让神经网络训练更快、更稳定的方法。 计算每个mini-batch的均值和方差，并将其拉回到均值为0方差为1的标准正态分布。 BN层通常在nonlinear function的前面/后面使用。返回

Depthwise_Conv2D

简述

depthwise_conv2d和conv2d的不同之处在于conv2d在每一深度上卷积，然后求和，depthwise_conv2d卷积，不求和。

区别

常规卷积操作

对于一张5×5像素、三通道（shape为5×5×3），经过3×3卷积核的卷积层（假设输出通道数为4，则卷积核shape为3×3×3×4，最终输出4个Feature Map， 如果有same padding则输出尺寸与输入层相同（5×5×4），如果没有则为尺寸变为3×3×4 Img 卷积层的参数数量可以用如下公式来计算：N_std = 4 × 3 × 3 × 3 = 108

逐通道卷积

一张5×5像素、三通道彩色输入图片（shape为5×5×3），Depthwise Convolution首先经过第一次卷积运算，DW完全是在二维平面内进行。卷积核的数量与上一层的通道数相同（通道和卷积核一一对应）。所以一个三通道的图像经过运算后生成了3个Feature map(如果有same padding则尺寸与输入层相同为5×5)。 Img 其中一个Filter只包含一个大小为3×3的Kernel，卷积部分的参数个数计算如下：N_depthwise = 3 × 3 × 3 = 27

Depthwise Convolution完成后的Feature map数量与输入层的通道数相同，无法扩展Feature map。

运算例子

Img

运算过程

Img

结果

Img

多卷积核过程

Img 返回

Dropout

Dropout说的简单一点就是：我们在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以使模型泛化性更强，因为它不会太依赖某些局部的特征 Img 返回

Pointwise Convolution

Pointwise Convolution的运算与常规卷积运算非常相似，它的卷积核的尺寸为 1×1×M，M为上一层的通道数。所以这里的卷积运算会将上一步的map在深度方向上进行加权组合，生成新的Feature map。有几个卷积核就有几个输出Feature map。 Img 由于采用的是1×1卷积的方式，此步中卷积涉及到的参数个数可以计算为： N_pointwise = 1 × 1 × 3 × 4 = 12

经过Pointwise Convolution之后，同样输出了4张Feature map，与常规卷积的输出维度相同。

参数对比

回顾一下，常规卷积的参数个数为： N_std = 4 × 3 × 3 × 3 = 108 Separable Convolution的参数由两部分相加得到： N_depthwise = 3 × 3 × 3 = 27 N_pointwise = 1 × 1 × 3 × 4 = 12 N_separable = N_depthwise + N_pointwise = 39

相同的输入，同样是得到4张Feature map，Separable Convolution的参数个数是常规卷积的约1/3。因此，在参数量相同的前提下，采用Separable Convolution的神经网络层数可以做的更深。 返回

无监督算法xDAWN + RG

提出了一种通过估计空间滤波器来增强P300诱发电位的无监督算法，pyRiemann网站 本文针对P300拼字脑接口中P300诱发电位增强的问题进行了研究。所提出的方法是无监督的，专门为P300拼写范例设计的:事实上，它只利用了视觉刺激的瞬间。

在初步研究中，我们展示了如何从原始脑电图信号中自动估计P300子空间。通过将原始脑电图投影到估计的P300子空间上，增强P300的诱发电位。

  1. 使用ERP模板串联方法训练两组5个xDAWN空间过滤器，每组用于二进制分类任务的每一类。
  2. 通过反向消除进行脑电图电极选择，只保留最相关的35个通道。
  3. 使用对数-欧氏度量将协方差矩阵投影到切空间上。
  4. 使用L1比值0.5进行特征归一化，表示L1和L2惩罚的权重相等。L1罚会使参数绝对值的总和变小，而L2罚会使参数的平方和变小。
  5. 使用弹性回归进行分类。

SMR分类

对于基于振荡的SMR分类，传统的方法是我们自己实现的One-Versus-Rest(OVR)滤波器组公共空间模式(FBCSP)算法

  1. 带通将脑电图信号以4Hz的步骤过滤为9个不重叠的滤波器组，从4Hz开始:4-8Hz, 8-12Hz，…, 36-40Hz。

  2. 由于分类问题是多类的，我们使用OVR分类，这需要我们为所有的OVR组合训练分类器，这里有4对OVR组合(第1类vs所有其他组合，第2类vs所有其他组合，等等)。我们使用自协方差收缩法[91]在训练数据上为每个滤波器组训练2对CSP滤波器(共4个滤波器)。这将为每次试验和每个OVR组合提供总共36个特征(9个滤波器组× 4个CSP滤波器)。

  3. 训练每个OVR组合的弹性网络逻辑回归分类器[92]。我们设弹性净罚α = 0.95。

  4. 找到最佳的λ值为弹性网络逻辑回归，以最大限度地验证通过在一个封闭的验证集上评估训练好的分类器来设置准确性。的多每次试验的标签是4个OVR中产生最大概率的分类器

  5. 使用步骤4中获得的λ值，将训练好的分类器应用到测试集。 Img

DeepConvNet架构

DeepConvNet架构，其中C =信道数，T =时间点数，N =类数。 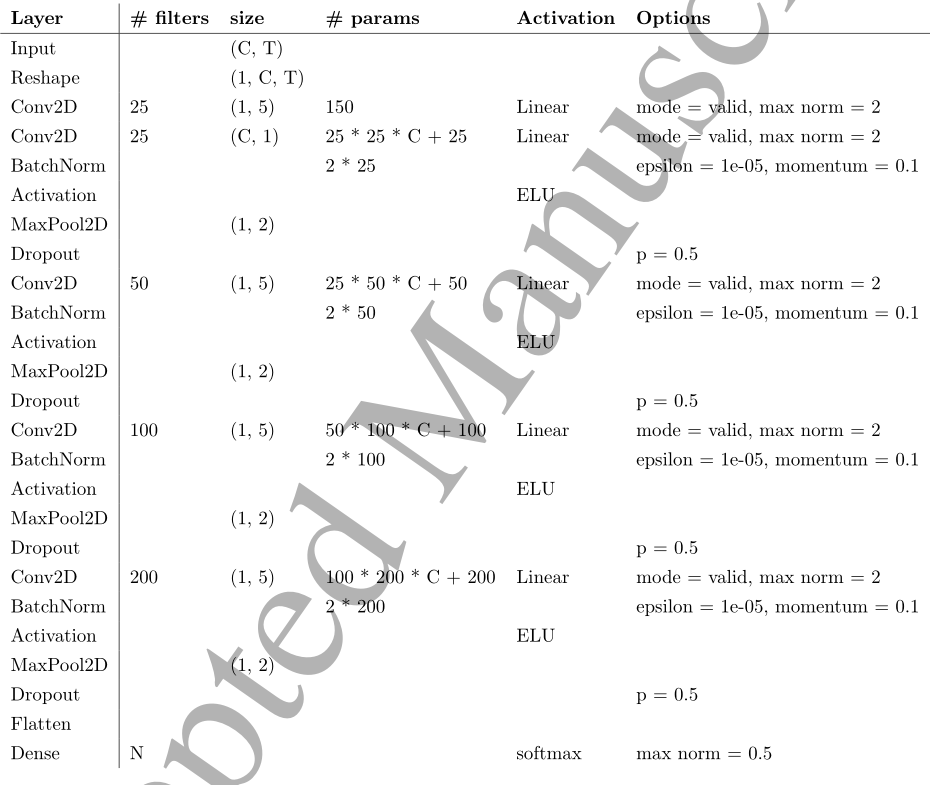Img

ShallowConvNet架构

ShallowConvNet架构，其中C =信道数，T =时间点数，N =类数。这里，"平方"和"log"激活函数分别为f(x) = x^2^和f(x) = log(x)。 Img

Img Img