锡林郭勒草原土壤物理性质和植被生物量影响的数学模型
机理建模
土壤水分变化厚度
侯琼等研究内蒙古典型草原模型时提出: 当年降水量较低时土壤水分入渗深度很少有超出100cm的现象 与此同时干旱年份的渗透深度甚至不足30cm。
这一点从附件3中的土壤湿度数据也不难看出, 如图所示, 200cm深度的土壤数据在2012年~2022年变化缓慢.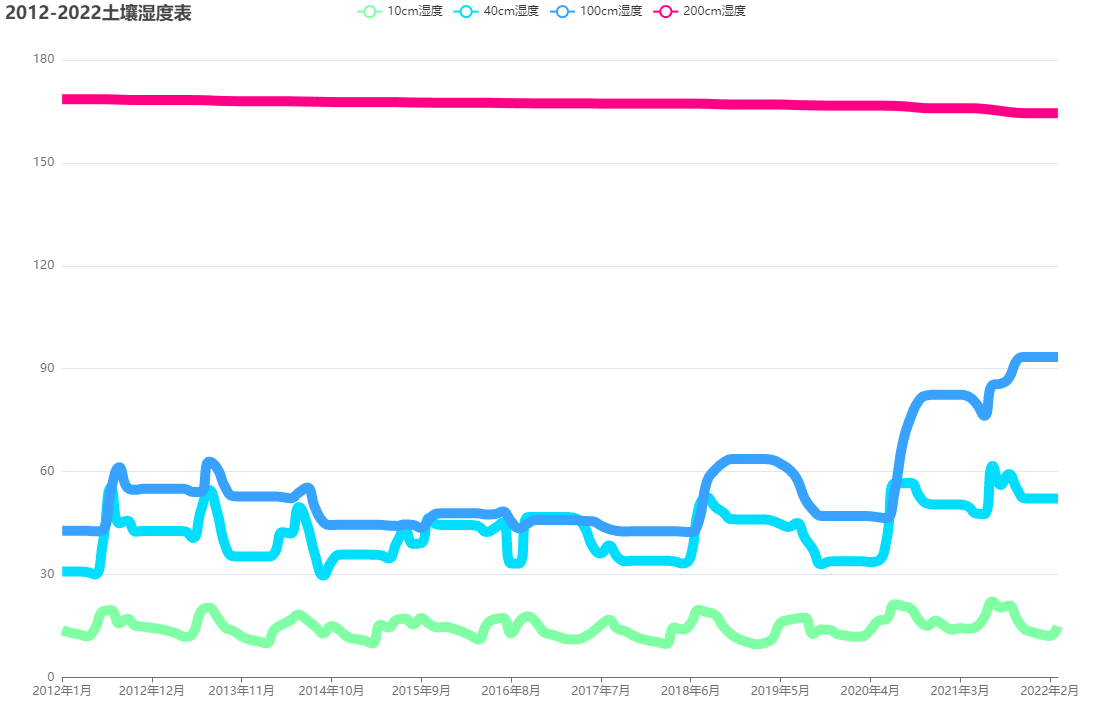 
所以对于土壤湿度的变化模型应当基于小于等于100cm的土壤深度范围建立.公式如下: \(W(t)=\int_{0-100 c m} \beta(t, h) d h\)
载畜率对植被生物量的作用的模型
根据Woodward等只考虑放牧影响,反映载畜率对植被生物量的作用的模型. \(\frac{dZ_w}{d t}=0.049 Z_w\left(1-\frac{Z_w}{4000}\right)-0.0047 S Z_w\)
| 符号 | 含义 |
|---|---|
| $Z_w$ | 植被生物量 |
| $S$ | 单位面积的载畜率 |
土壤-植被-大气系统的水平衡基本方程
草原水分通过降水、入渗、蒸发等形式周而复始的循环，其过程十分复杂，在无人干扰的情况下，土壤-植被-大气系统的水平衡基本方程为 \(\Delta W=W_{t+1}-W_{t}=P+G_{u}+R_{i n}-\left(E t_{a}+G_{d}+R_{\text {att }}+I C_{\text {stree }}\right)\)
| 符号 | 含义 |
|---|---|
| $\Delta W$ | 土壤贮水变化量 |
| $W_{t+1},W_{t}$ | 时间段内的始末土壤含水量 |
| $P$ | 降水量 |
| $G_u,G_d$ | 分别为地下水毛管上升量和土壤水渗透量 |
| $Et_a$ | 实际蒸发量 |
| $R_{in} ,R_{out}$ | 分别为入和出径流量 |
在文献中,侯琼等研究者指出在整个草原区域内其出入径流可视为相 等,则可以通过$R_{in} = R_{out}$和$G_d=0$来简化模型, 简化后的模型为: \(\Delta W=P-(E t_{a}+G_{d}+I C_{\text {store }})\)
植被覆盖率与截流量
植被截流量与降水量、植被覆盖度、叶面积指数（LAI）等密切相关。植被覆盖率是植物群落覆盖地表状况的一个综合量化指标，能够直观反映地表植被的丰度。降水量小、植被覆盖度高、LAI大时植被截流量大，其表达式为： \(I C_{\text {store }}=c_{p} \cdot I C_{\max } \cdot\left[1-\exp \left(-k \cdot R_{\text {cum }} / I C_{\max }\right)\right]\) |符号|含义| |–|–| |$IC_{store}$|植被截流量（mm）| |$c_p$ |植被覆盖率| |$IC_{max}$|特定植被的最大截流量（mm）| |$k$ |植被密度校正因子与 $LAI$ 有关| |$R_{cum}$ |累积降雨量（mm）|
$IC_{max}$可以通过 $LAI$ 来估算：
\[I C_{\max }=0.935+0.498 \cdot L A I-0.00575 \cdot L A I^{2}\] \[L A I=a \cdot \exp (k \cdot N D V I)\]| 符号 | 含义 |
|---|---|
| $N D V I$ | 植被指数 |
| $LAI$ | 叶面积指数 |
本文构建$C_p$的公式由$覆盖率=（增长率-枯萎率-吃掉的）*盖度$给出,1.8代表题目给的一只羊吃掉的生物量，家畜日食量为1.8kg，即标准羊单位, 具体公式如下: \(c_{p}(t)=\left[\alpha^{*}-W\left(e^{\varepsilon_g, w(t) / w^{*}}-1\right)-1.8 S(t)\right]\left(1-e^{-\varepsilon, \varepsilon^{g}(t) / w^{*}}\right)\)
总结
综上所述,我们可以将模型总结为如下形式 \(\left\{\begin{array}{l}\frac{d Z_w(t)}{d t}=a Z_w(t)\left(1-\frac{Z_w(t)}{b}\right)-c S(t)Z_w(t) \\\Delta W=P-\left(E t_{a}+G_{d}+I C_{\text {store }}\right) \\ I C_{\text {store }}(t)=c_{p}(t) \cdot I C_{\max }(t) \cdot\left[1-\exp \left(-k \cdot P(t) / I C_{\max }(t)\right)\right] \\ I C_{\max }(t)=0.935+0.498 \cdot L A I(t)-0.00575 \cdot L A I(t)^{2} \\ c_{p}(t)=\left[\alpha^{*}-W\left(e^{\varepsilon_g, w(t) / w^{*}}-1\right)-1.8 S(t)\right]\left(1-e^{-\varepsilon, \varepsilon^{g}(t) / w^{*}}\right) \\ L A I(t)=a \cdot \exp (k \cdot N D V I) \\ W(t)=\int_{0-100 c m} \beta(t, h) d h \end{array}\right.\)
| 符号 | 含义 |
|---|---|
| $a,b,c$ | 未知系数, 由放牧环境所确定的常数 |
| $S(t)$ | 自变量, 单位面积载畜率, 不放牧就是0 |
| $W$ | 因变量, 土壤含水量 |
| $t$ | 月份 |
| $\beta$ | 湿度 |
| $h$ | 深度 |