基于小波的单通道脑电数据无监督眼伪影去除技术比较研究
伪影干扰
脑电图信号经常被两种伪影破坏:生理的,如眼睛、肌肉和心脏活动,以及生理外的,如线干扰和电极噪声。由于存在光谱分离,生理外伪影通常可以通过适当的滤波技术去除。但是生理伪影去除需要仔细注意,因为它们可能在脑电图信号的相同频率范围内,并且是非周期性的。由眼球运动和眨眼引起的眼伪影OA比其他污染性生理伪影占主导地位。
去OA的几种方法
- 基于时域和频域的回归
- 统计技术如主成分分析(PCA)
- 独立成分分析(ICA)
- 多尺度样本熵
- 应用SWT和coif3小波滤波器对脑电信号去噪
- 以sym3为基函数的SWT,利用变异系数对人眼伪影进行检测和去噪。
已有方案比较
以上几种方法依赖于多通道数据。小波变换WT是单通道脑电图数据鲁棒且有前景的眼伪影去除技术之一。
基函数选择
- haar
- coif3
- sym3
- bior4.4

小波变换
原理
小波变换可以应用于任何单通道脑电数据,去除OAs,而不需要任何其他脑电或脑电通道的信息。小波变换将时变信号分解为一组基函数,即小波。这些基函数被称为小波,是通过对母小波进行扩张和移动得到的:  式中,
式中,a为缩放参数,b为移位参数。
离散小波变换DWT
DWT被认为是一种非冗余高效的小波变换,可以获得信号的离散小波表示。在DWT中,输入信号经过低通滤波器和高通滤波器,分别得到近似系数ak和细节系数dk,其中k表示分解级别。这个过程重复,直到得到所需的频率范围。在每个阶段,滤波器输出被二次采样,然后采样重建信号。在本研究中,我们使用Matlab中的内置wavedec函数实现去噪算法中的DWT。
平稳小波变换SWT
主要缺点是它的时间方差,这在统计信号处理应用中特别重要。SWT克服了DWT的转换不变性缺点,但具有冗余信息,且相对较慢。
差异
DWT和SWT的设计差异在于每一级的滤波器。每一层分解的近似序列和细节序列与原始序列长度相同。在得到第j层的系数后,算法向上对滤波系数进行2j−1的采样。本研究利用MATLAB中的swt函数实现了该算法。
阈值函数
小波阈值降噪对脑电信号分解后的近似系数和细节系数进行降噪,将人工系数从神经信号系数中分离出来。对于小波系数的阈值,本文采用通用阈值(Universal Threshold, UT)和统计阈值(Statistical Threshold, ST)两种常用的阈值进行了评估。

| 名称 | 说明 |
|---|---|
K | 对神经元宽带信号幅值的估计,阈值 |
N | 待处理数据的长度,样本个数 |
Ca | 经过阈值处理的第ath级分解小波系数 |
0.6745 | 高斯噪声的常数值 |
median | 中值 |

| 名称 | 说明 |
|---|---|
T | 利用ST估计神经元宽带信号的大小 |
std(Hk) | 采用第k级小波系数的标准差 |
阈值法
这两种情况都采用硬阈值法,当小波系数绝对值大于阈值时,就去除小波系数。
性能指标
| 名称 | 公式 | 说明 |
|---|---|---|
相关系数 |  | 表明两个变量之间的关联程度 |
互信息 |  | 用来衡量一随机变量包含多少另一随机变量的信息 |
信伪比 |  | 用于测量经过算法处理后的特定信号中伪影去除量。注 |
归一化均方误差 |  | 近似理想数据与实际数据之间的差异 |
结果
比较了使用coif3小波基函数和统计阈值对单通道EEG数据进行SWT和DWT去噪的,原始和无oa伪迹EEG数据。仔细观察表明,SWT产生了更干净的处理信号,然而,DWT是一种更快的方法,这是实时数据处理(如流数据)的一个重要方面。大多数OA去除算法会影响没有闪烁伪影的神经元信号(非闪烁区域)。为了提高去除OA算法的区分性能,在保留神经元信号的同时,我们将原始脑电图数据划分为"眨眼区域"和"非眨眼区域"。 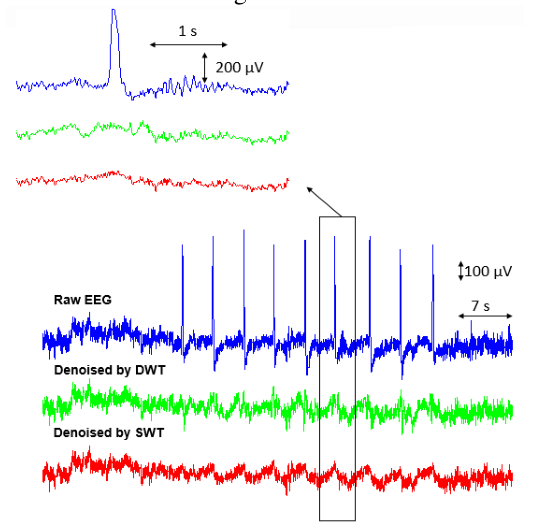
结论
由于这些指标分析了算法的不同性能,所以在所有指标的基础上,没有一种组合是更好的。
- 利用coif3和bior4.4小波基函数进行ST小波变换,可以很好地去除OA
- 基于CC、MI、SAR、NMSE和时频分析保留非眨眼区域的神经元信号
- 在实时分析方面DWT比SWT需要更少的计算资源。
结果表明,DWT+ST+coif3或DWT+ST+bior4.4可能是最优选择。
如果不在乎计算时间,可以使用带有统计阈值的haar小波SWT。
source: test_long/folder1/2.基于小波的单通道脑电数据无监督眼伪影去除技术比较研究.md