RNN

从单层网络到经典的RNN结构

单层网络

在学习LSTM之前，得先学习RNN，而在学习RNN之前，首先要了解一下最基本的单层网络，它的结构如下图所示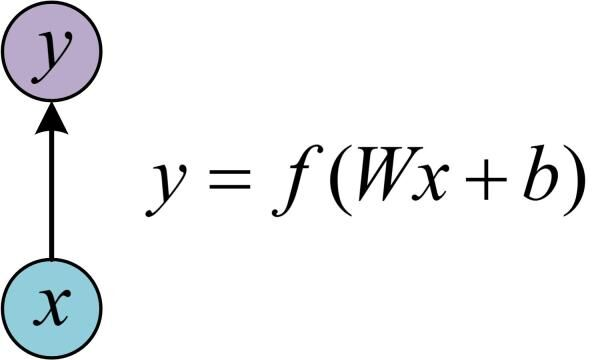：输入是x，经过变换Wx+b和激活函数f，得到输出y。相信大家对这个已经非常熟悉了。在实际应用中，我们还会遇到很多序列形的数据：

::: tip 例子

自然语言处理问题。x1可以看做是第一个单词，x2可以看做是第二个单词，依次类推。
语音处理。此时，x1、x2、x3……是每帧的声音信号。
时间序列问题。例如每天的股票价格等等。 :::

而其中，序列形的数据就不太好用原始的神经网络处理了。为了建模序列问题，RNN引入了==隐状态h==（hidden state）的概念，h可以对序列形的数据提取特征，接着再转换为输出。

计算

先从H~1~的计算开始看：

记号	含义
圆圈或方块	向量
箭头	表示对该向量做一次变换

H~2~的计算和H~1~类似。但有两点需要注意下：

在计算时，每一步使用的参数U、W、b都是一样的，也就是说每个步骤的==参数都是共享的==，这是RNN的重要特点，一定要牢记；
但是==LSTM中的权值==则不共享，因为它是在两个不同的向量中。而RNN的权值为何共享呢？很简单，因为RNN的权值是在同一个向量中，只是不同时刻而已。

依次计算剩下来的（使用相同的参数U、W、b）：

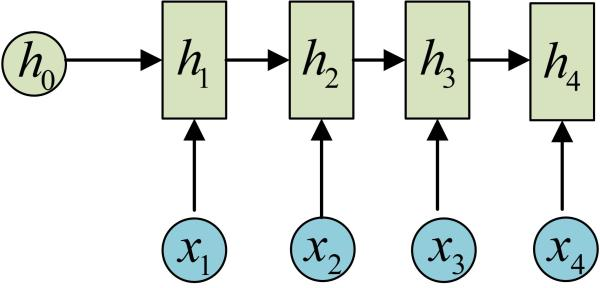
我们这里为了方便起见，只画出序列长度为4的情况，实际上，这个计算过程可以无限地持续下去。

我们目前的RNN还没有输出，得到输出值的方法就是直接通过h进行计算：

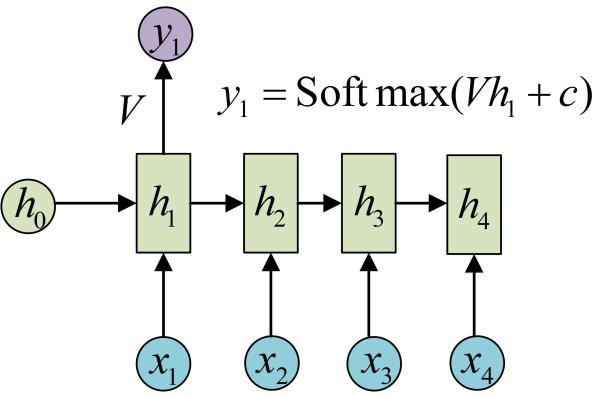
正如之前所说，一个箭头就表示对对应的向量做一次类似于f(Wx+b)的变换，这里的这个箭头就表示对==h1==进行一次变换，得到输出==y1==。

剩下的输出类似进行（使用和y1同样的参数V和c）：

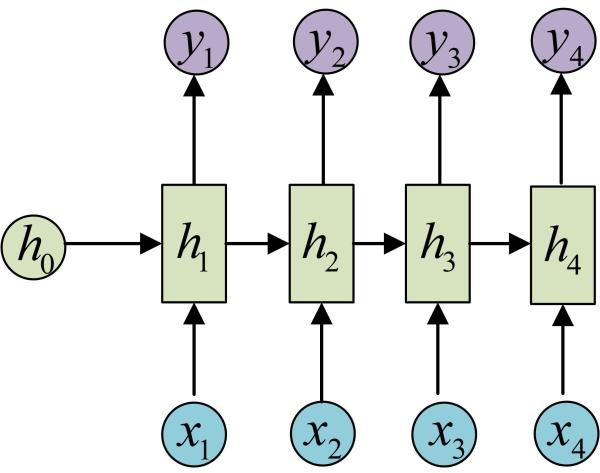
OK！大功告成！这就是最经典的RNN结构，是x1, x2, …..xn，输出为y1, y2, …yn，也就是说，输入和输出序列必须要是==等长==的。

RNN的应用

传统网络的弊端

人类并不是每时每刻都从一片空白的大脑开始他们的思考。在你阅读这篇文章时候，你都是基于自己已经拥有的对先前所见词的理解来推断当前词的真实含义。我们不会将所有的东西都全部丢弃，然后用空白的大脑进行思考。我们的思想拥有==持久性==。

传统的神经网络并不能做到这点，看起来也像是一种==巨大的弊端==。 ::: tip 例子假设你希望对电影中的每个时间点的时间类型进行分类。传统的神经网络应该很难来处理这个问题：使用电影中先前的事件推断后续的事件。 ::: 循环神经网络RNN解决了这个问题。

循环展开

通过上文第一节我们已经知道，RNN是包含==循环==的网络，在这个循环的结构中，每个神经网络的模块A，读取某个输入x~i~，并输出一个值h~i~（注：输出之前由y表示，从此处起，改为隐层输出h表示）。

然后不断循环。循环可以使得信息可以从当前步传递到下一步。

这些循环使得RNN看起来非常神秘。然而，如果你仔细想想，这样也不比一个正常的神经网络难于理解。RNN可以被看做是同一神经网络的多次复制，每个神经网络模块会把消息传递给下一个。所以，如果我们将这个循环展开：

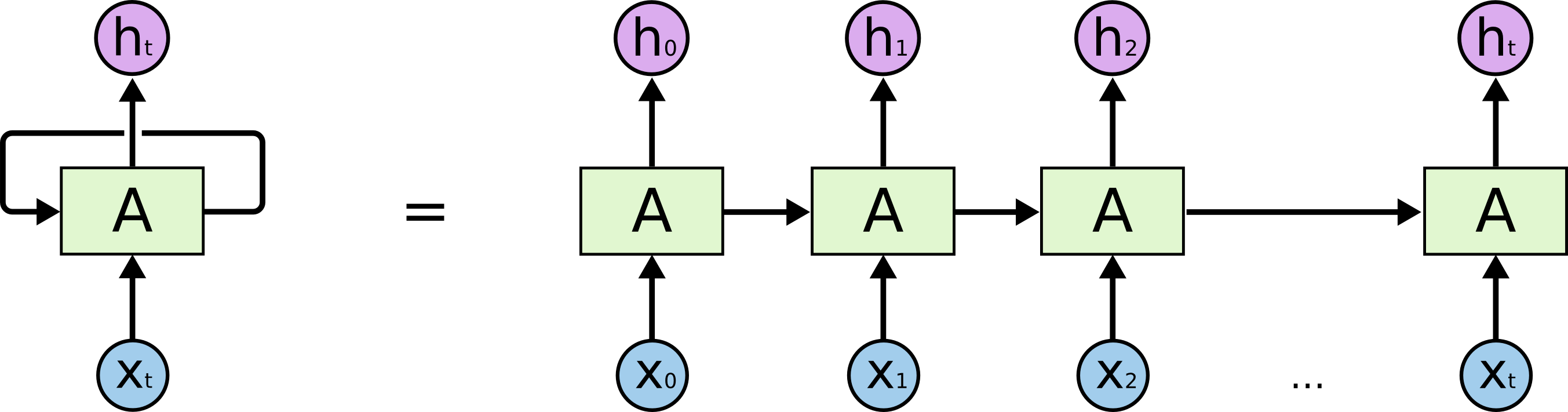
链式的特征揭示了RNN本质上是与序列和列表相关的。他们是对于这类数据的最自然的神经网络架构。

RNN的局限：长期依赖问题

先前的信息

RNN的关键点之一就是他们可以用来==连接先前的信息到当前的任务==上，例如使用过去的视频段来推测对当前段的理解。如果RNN可以做到这个，他们就变得非常有用。但是真的可以么？答案是，还有很多依赖因素。

有时候，我们仅仅需要知道先前的信息来执行当前的任务。例如，我们有一个语言模型用来基于先前的词来预测下一个词。如果我们试着预测==the clouds are in the sky==最后的词，我们并不再需要其他的信息，因为很显然下一个词应该是==sky==。在这样的场景中，相关的信息和预测的词位置之间的间隔是非常小的，RNN可以学会使用先前的信息。

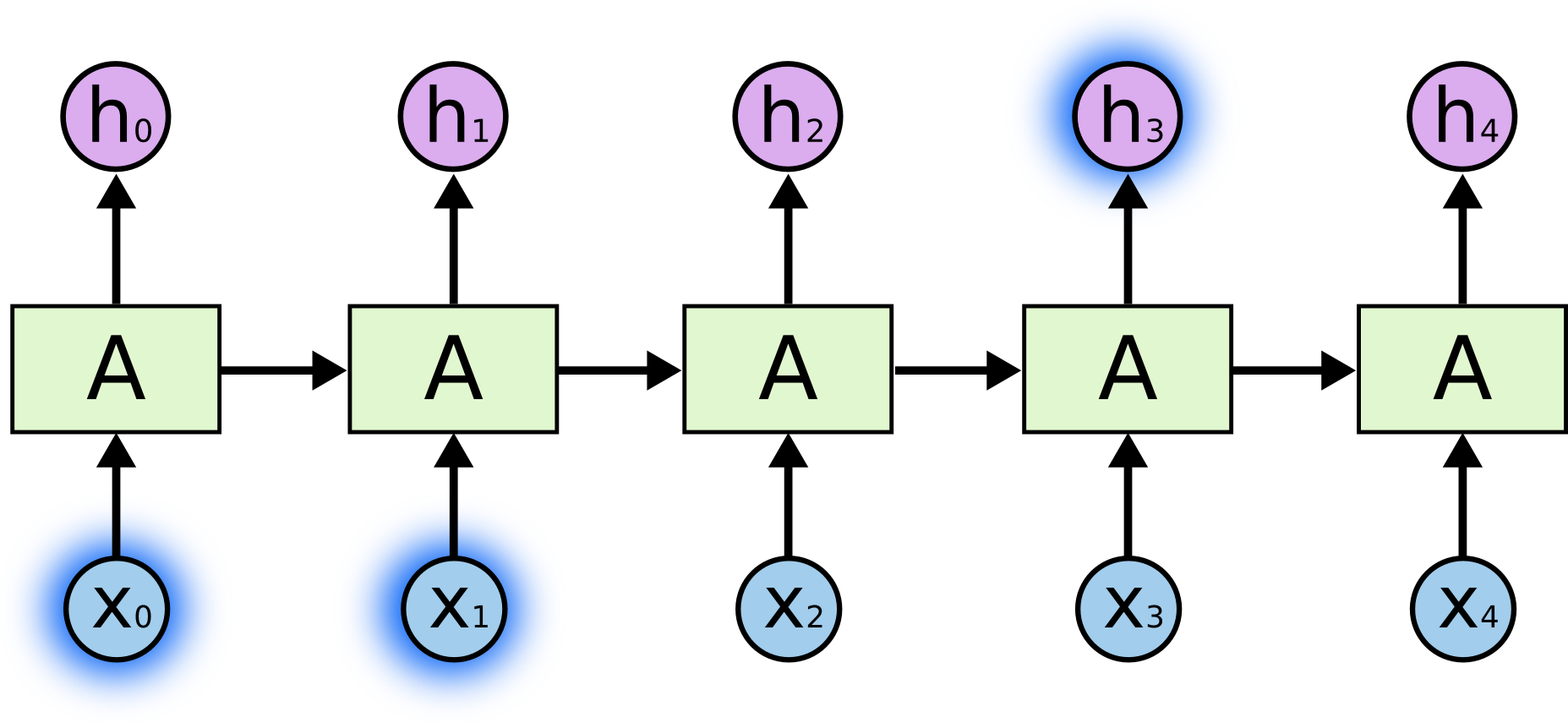
但是同样会有一些更加复杂的场景。假设我们试着去预测==I grew up in France…I speak fluent French==最后的词。当前的信息建议下一个词可能是一种语言的名字，但是如果我们需要弄清楚是什么语言，我们是需要先前提到的离当前位置很远的==France==的上下文的。这说明相关信息和当前预测位置之间的间隔就肯定变得相当的大。

不幸的是，在这个间隔不断增大时，RNN会丧失学习到连接如此远的信息的能力。

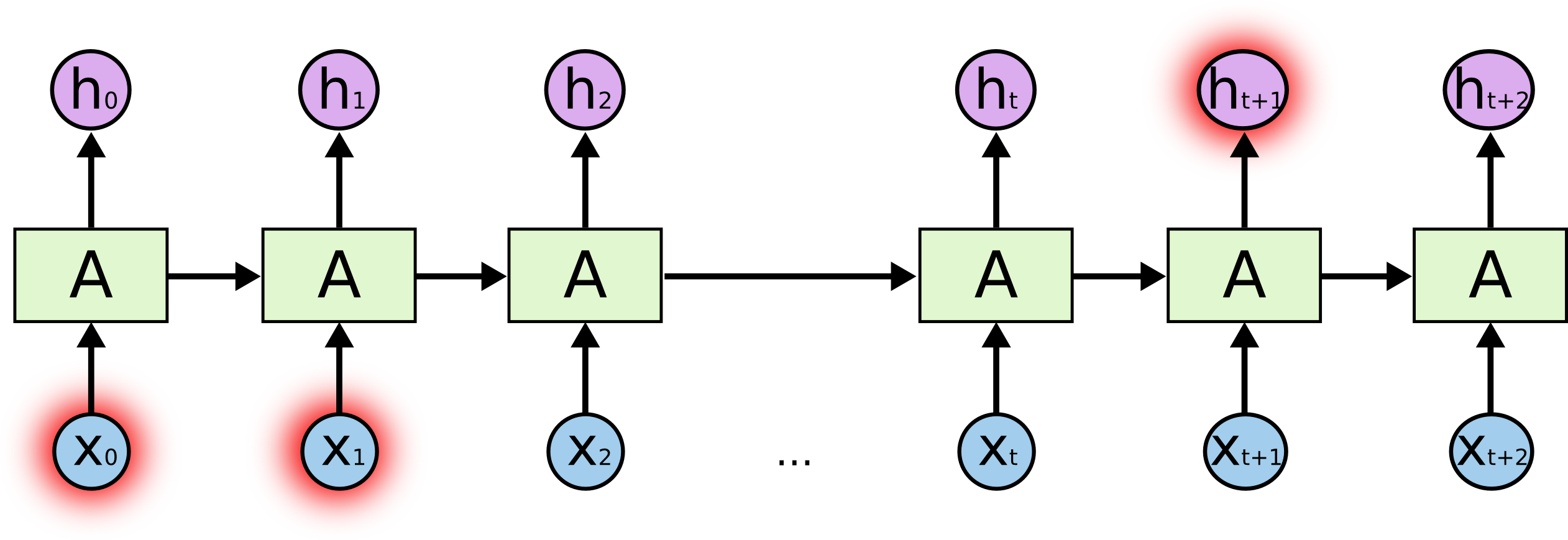
结论

在理论上，RNN绝对可以处理这样的长期依赖问题。人们可以仔细挑选参数来解决这类问题中的最初级形式，但在实践中，RNN肯定不能够成功学习到这些知识。Bengio,etal.(1994)等人对该问题进行了深入的研究，他们发现一些使训练RNN变得非常困难的相当根本的原因。换句话说， ::: tip 根本原因 RNN 会受到短时记忆的影响。如果一条序列足够长，那它们将很难将信息从较早的时间步传送到后面的时间步。 ::: 因此，如果你正在尝试处理一段文本进行预测，RNN 可能从一开始就会遗漏重要信息。在反向传播期间，RNN 会面临梯度消失的问题。 ::: tip 反向传播反向传播是一个很重要的核心议题，本质是通过不断缩小误差去更新权值，从而不断去修正拟合的函数 :::

因为梯度是用于更新神经网络的权重值 ==新的权值 = 旧权值 - 学习率*梯度==，梯度会随着时间的推移不断下降减少，而当梯度值变得非常小时，就不会继续学习。

换言之， ::: tip 总结在递归神经网络中，获得小梯度更新的层会停止学习—— 那些通常是较早的层。由于这些层不学习，RNN 可以忘记它在较长序列中看到的内容，因此具有短时记忆。 ::: 而==梯度爆炸==则是因为计算的难度越来越复杂导致。

然而，幸运的是，有个RNN的变体——LSTM，可以在一定程度上解决梯度消失和梯度爆炸这两个问题！来源