一些方法简介
逻辑回归
简单来说, 逻辑回归(Logistic Regression)是一种用于解决二分类(0 or 1)问题的机器学习方法,用于估计某种事物的可能性。 逻辑回归假设因变量 y 服从伯努利分布,而线性回归假设因变量 y 服从高斯分布。 因此与线性回归有很多相同之处,去除Sigmoid映射函数的话,逻辑回归算法就是一个线性回归。可以说,逻辑回归是以线性回归为理论支持的,但是逻辑回归通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题。
逻辑回归的假设函数形式如下:
\(h_\theta(x) = g(\theta^T x), g(z)= \frac{1}{1+e^{-z}}\) 所以:
\(h_\theta(x)= \frac{1}{1+e^{-\theta^Tx}}\) 其中 x 是我们的输入, $\theta$ 为我们要求取的参数。
一个机器学习的模型,实际上是把决策函数限定在某一组条件下,这组限定条件就决定了模型的假设空间。当然,我们还希望这组限定条件简单而合理。而逻辑回归模型所做的假设是:
\(P(y=1|x;\theta) =g(\theta^Tx)= \frac{1}{1+e^{-\theta^Tx}}\) 这个函数的意思就是在给定 $x$ 和 $\theta$的条件下 $y=1$ 的概率。
这里 $g(h)$ 就是sigmoid函数,与之相对应的决策函数为:
\(y^* = 1, if P(y=1|x)>0.5\) 选择0.5作为阈值是一个一般的做法,实际应用时特定的情况可以选择不同阈值,如果对正例的判别准确性要求高,可以选择阈值大一些,对正例的召回要求高,则可以选择阈值小一些。
LSTM
简介
长短时记忆网络(LSTM)是一种特殊的递归神经网络(RNN);它非常擅长处理序列数据, 是一种RNN特殊的类型,可以学习长期依赖信息。当然,LSTM和基线RNN并没有特别大的结构不同,但是它们用了不同的函数来计算隐状态。
组成
LSTM网络由==细胞==组成,细胞的输出根据过去的记忆内容通过网络演进。
这些细胞有一个共同的细胞状态,在整个细胞LSTM链上保持长期依赖关系。然后,信息流由==输入门==(it)和==忘记门==(ft)控制,从而允许网络决定是忘记之前的状态$C_{t-1}$还是用新信息更新当前状态$C_{t}$。每个单元的输出(隐藏状态)由一个==输出门==$o_{t}$控制,允许单元计算其输出给定更新的单元状态.

描述LSTM单元结构的公式如下: \(\mathbf{i}_{\mathbf{t}}=\sigma\left(\mathbf{W}_{\mathbf{i}} \cdot\left[\mathbf{h}_{\mathbf{t}-\mathbf{1}}, \mathbf{x}_{\mathbf{t}}\right]+\mathbf{b}_{\mathbf{i}}\right)\) \(\mathbf{f}_{\mathbf{t}}=\sigma\left(\mathbf{W}_{\mathbf{f}} \cdot\left[\mathbf{h}_{\mathbf{t}-\mathbf{1}}, \mathbf{x}_{\mathbf{t}}\right]+\mathbf{b}_{\mathbf{f}}\right)\) \(\mathbf{C}_{\mathbf{t}}=\mathbf{f}_{\mathbf{t}} * \mathbf{C}_{\mathbf{t}-\mathbf{1}}+\mathbf{i}_{\mathbf{t}} * \tanh \left(\mathbf{W}_{\mathbf{c}} \cdot\left[\mathbf{h}_{\mathbf{t}-\mathbf{1}}, \mathbf{x}_{\mathbf{t}}\right]+\mathbf{b}_{\mathbf{c}}\right)\) \(\mathbf{o}_{\mathbf{t}}=\sigma\left(\mathbf{W}_{\mathbf{o}} \cdot\left[\mathbf{h}_{\mathbf{t}-\mathbf{1}}, \mathbf{x}_{\mathbf{t}}\right]+\mathbf{b}_{\mathbf{o}}\right)\) \(\mathbf{h}_{\mathbf{t}}=\mathbf{o}_{\mathbf{t}} * \tanh \left(\mathbf{C}_{\mathbf{t}}\right)\)
\[\sigma(x)=\frac{1}{1+e^{-x}}, \tanh (x)=\frac{2}{1+e^{-2 x}}-1\]| 名称 | 描述 |
|---|---|
| $h_t$ | 是时间步长t时的隐藏状态 |
| $C_{t-1}$ | 是时间步长t时的细胞状态 |
| $x_t$ | 是馈入细胞的输入特征 |
| $W_f$, $W_i$, $W_c$, $W_o$ | 是权重 |
| $b_f$, $b_i$, $b_c$, $b_o$ | 是通过时间反向传播可以得到的偏差 |
参数设置
LSTM的超参数会影响模型的分类性能,我们没有选择更深的LSTM层的原因是为了防止过度拟合。
| 名称 | 描述 |
|---|---|
| 每层细胞数量 | 300 |
| LSTM单元的dropout | 50% |
| LSTM层的数量 | 2 |
| 激活函数 | ReLu |
随机森林
随机森林顾名思义,是用随机的方式建立一个森林,森林里面有很多的决策树组成,随机森林的每一棵决策树之间是没有关联的。在得到森林之后,当有一个新的输入样本进入的时候,就让森林中的每一棵决策树分别进行一下判断,看看这个样本应该属于哪一类(对于分类算法),然后看看哪一类被选择最多,就预测这个样本为那一类。
决策树(decision tree)
是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
随机森林由决策树组成,决策树实际上是将空间用超平面进行划分的一种方法,每次分割的时候,都将当前的空间一分为二
下面是随机森林的构造过程:
1. 假如有N个样本,则有放回的随机选择N个样本(每次随机选择一个样本,然后返回继续选择)。这选择好了的N个样本用来训练一个决策树,作为决策树根节点处的样本。
2. 当每个样本有M个属性时,在决策树的每个节点需要分裂时,随机从这M个属性中选取出m个属性,满足条件m « M。然后从这m个属性中采用某种策略(比如说信息增益)来选择1个属性作为该节点的分裂属性。
3. 决策树形成过程中每个节点都要按照步骤2来分裂(很容易理解,如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性,则该节点已经达到了叶子节点,无须继续分裂了)。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
4. 按照步骤1~3建立大量的决策树,这样就构成了随机森林了。
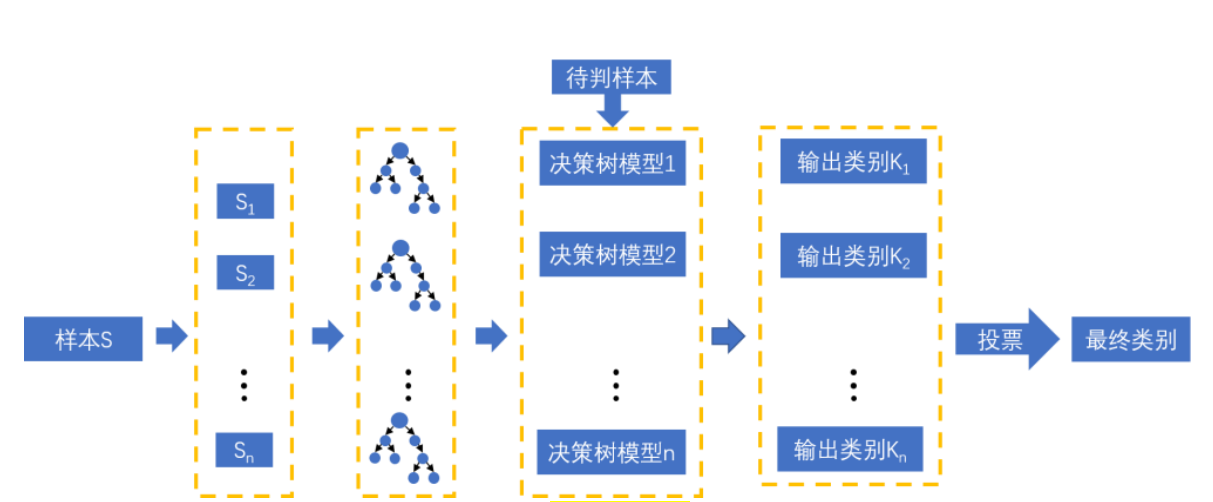
图 5.5 随机森林结构 随机森林变量选择过程如表 5-4 所示。  ::: tip这个在参考论文D21103000002.pdf里面 :::
::: tip这个在参考论文D21103000002.pdf里面 :::
XGBoost
极端梯度提升树(XGBoost) 极端梯度提升树是一种集成机器学习算法,其在传统提升树的基础上引入正则化项来控制复杂度,对代价函数做二阶 Talor 展开,并对树结构进行一定变换,使整个代价函数由组成树的数量表示。XGBoost 能自动学习分裂方向,支持各种抽样。XGBoost 的目标函数为: \(o b j^{*}=-\frac{1}{2} \sum_{j=1}^{T} \frac{G_{j}}{H_{j}+\lambda}+\gamma \mathcal{N}\) 式中𝒩𝒩表示数的子节点的个数。本题使用开源 python 库 xgboost 进行模型搭建,对决策树最大深度、𝛾、𝜆等参数使用人工调参方法进行模型训练,评价方法采用 5 折交叉验证。