基于DWT的脑电信号癫痫发作k-NN分类器检测

摘要

本研究提出了一种利用记录的脑电图信号检测健康人与癫痫患者癫痫发作的框架。利用Simulink对脑电信号进行建模，采用离散小波变换(DWT)进行脑电信号的分解和统计计算;使用Xilinx系统生成器在FPGA上实现。经过DWT分解，提取均值绝对值(Mean Absolute Value, MA)、标准差(Standard Deviation, SD)和平均功率(Average power, AP)作为统计特征，利用k-NN分类器进行癫痫检测。结果表明，在提取特征数量较少的情况下，k-NN分类器对睁眼数据集和癫痫发作数据集分别采用标准差和标准差结合MA进行分类，具有较好的分类精度。

对于从脑电图信号检测癫痫、阿尔茨海默病等疾病，脑电图信号被分解为各种波段，如delta (0-4 Hz)、theta (4-8 Hz)、alpha(8-16 Hz)和beta (16-32 Hz)。对于信号的频率分析，我们可以使用信号的傅里叶变换。但是，脑电信号具有非平稳、非线性的特点，傅里叶变换(FT)不适用于非平稳信号。因此，可以采用短时傅里叶变换(STFT)。STFT的缺点是窗口长度有限，分辨率不高。这个问题可以用小波变换来解决。它用一个叫做"小波"的窗函数的平移和扩张来取代FT的正弦波。小波变换有两种:离散小波变换(DWT)和连续小波变换(CW)。冗余是CWT的主要问题。因此，DWT被用于小波分解。

DWT是一种利用小波进行信号分解的非冗余高效变换。 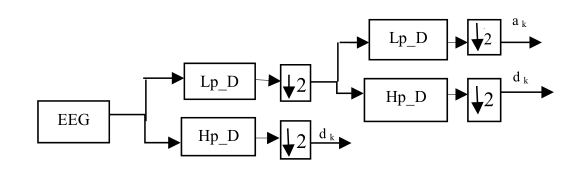Img

为了得到详细的(dk)和近似的(ak)系数，信号被应用于高通和低通滤波器，直到得到所需的频率范围。每个滤波输出按2向下采样。

性能指标

名称 公式 说明
平均绝对值(MA) 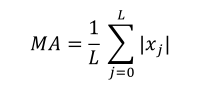Img 是信号频率信息的量度
平均功率(AP) Img 给出有关信号频率内容的信息
标准差(SD) Img 表示信号频率变化幅度
其中xj表示EEG数据集中的第j个样本，μ表示中值，L表示分段长度。{colspan=3}    

流程

预处理

脑电信号通过低通滤波器将频率限制在64hz以内

小波变换

对信号进行频带分解，利用MATLAB对symlet4小波提取其系数，通过高通滤波器和低通滤波器对信号进行分解。

KNN分类

进行特征提取后，采用K-NN分类器对个体特征和组合特征进行分类。从灵敏度、特异性和准确性三个方面分析了分类器的性能。

KNN

k-NN分类器是一种相对简单的非线性非参数分类器。分类需要大量的训练和测试数据集。它基于训练数据集和测试数据集之间的相似性。m特征按数据集分类。基于训练的k近邻数据集，将测试数据集分配给一个类。数据集的接近度以欧氏距离(ED)计算 Img 通过计算灵敏度、选择性和精度作为k-NN分类器的性能参数。

结果

对于P-T数据集，SD和SD结合MA特征均可获得100%的准确率。对于数据集Q-T, MA特征和AP+SD组合特征的最高精度为99.2%。数据集R-T采用SD和AP+SD组合特征，精度最高可达99.11。对于数据集S-T, MA特征和AD+SD组合特征的精度最高可达95.70%。PQ-T数据集，以MA为特征，获得的最高精度为98.86%。采用MA+SD对数据集QR-T进行分析，获得99.3%的精度。对于数据集PRS-T, SD特征的准确率最高，达到96.4%;对于数据集QRS-T, SD特征的准确率最高，达到96.7%。从表中可以看出，k-NN分类器通过从DWT系数中分离或组合特征来提高性能。

补充

连续小波变换（Continuous Wavelet Transform, CWT）

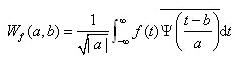Img 这就是信号f(t)的连续小波变换公式，其中参数a和b都是连续变化的参数，a为尺度参数（在某种意义上就是频率的概念），b是时间参数或平移参数。不严谨地讲，Wf(a,b)指的是对信号f(t)进行小波变换后当频率为a时间为b时的变换值。可以看出，一维信号f(t)经过小波变换后将变成二维信号。

离散小波变换（Discrete Wavelet Transform, DWT）

我们关注离散小波变换多数情况实际上是得到一个类似于离散傅里叶变换DFT的变换，时域和变换域都是离散有限长的，方便计算机处理。然而，DWT指的是将CWT中的尺度参数a和平移参数b离散化。这里要特别注意：DWT并没有将信号f(t)和小波ψ(t)中的时间变量t离散化！这与DFT的概念是非常不一样的！！

在尺度参数a和平移参数b离散过程中，一般对尺度进行幂数级离散化，即令a=a0m，对b均匀离散，考虑到不同尺度下频率不同，因此不同尺度下参数b的离散间隔不同。

二进小波变换（Dyadic Wavelet Transform）

前面提到，离散小波变换是对尺度参数a和平移参数b都进行了离散化，一般对尺度进行幂数级离散化，即令a=a0m，若特殊化取a0=2，然后保持平移参数b仍是连续的，则这类小波我们称为二进小波变换。总结起来，二进小波变换的概念介于CWT和DWT之间：相比于CWT，二进小波变换的尺度参数是特殊离散化的（a=2m）；相比于DWT，二进小波变换的尺度参数不能随意离散，而是特殊离散化的（a=2m），平移参数b是保持连续变化。

离散序列的小波变换

到这里有必要提一下正交小波变换，前面说了三种小波变换，但它们的小波基都不是正交的，这会带来一些麻烦，通过它们对信号变换后的信息是有冗余的，因此构建正交小波基是有重要意义的。Mallat给出了一种在正交小波基上的信号分解算法，也就是著明的Mallat算法了。

离散序列的小波变换就是基于著明的Mallat算法，实际上Mallat算法也是针对连续信号的，但在每一层的分解过程中（这里说的每一层实际上就是前面尺度的概念），各层分解系数之间有着某种关系，什么关系呢？那就看看Mallat算法框图吧，如下图所示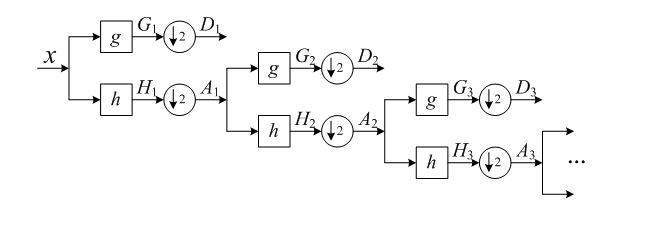： Img 初始系数x（暂且这么称呼）与其第一层分解后的高频系数D1（细节部分Detail）的关系是x经过高通滤波器g滤波后再下采样，与低频系数A1（近似部分Approximate）的关系是x经过低通滤波器h滤波后再下采样；

然后继续对低频系数A1进行第二层分解，低频系数A1与其第二层分解后的高频系数D2（细节部分Detail）的关系是A1经过高通滤波器g滤波后再下采样，与低频系数A1（近似部分Approximate）的关系是A1经过低通滤波器h滤波后再下采样；

后面依次类推即可。由于一直在下采样，所以虽然滤波器系数g和h不变，但其滤波带宽一直在减半。初始系数是怎么来的呢？肯定是根据信号得到的，最简单最粗糙的办法就是对信号直接抽样。这是对连续信号进行正交小波分解，有了这些系数，再利用正交小波基，就可以表示出信号了，这类似于连续周期信号的傅里叶级数分解吧。

从Matllat算法的框图可以看出，从始至终这是对离散序列x再进行变换分解，即初始系数即是离散信号x，经过多层分解后最后各分解系数合起来就是变换的结果。