对于EEG信号SWT与Butterworth滤波器比较
EEG信号分类
| 名称 | 频段 | 说明 |
|---|---|---|
| $\delta$ | (0.4-4Hz) | |
| $\theta$ | (4-8Hz) | θ波代表冥想、活动改善、记忆增强和压力降低 |
| $\alpha$ | (8-13Hz) | α节律代表稳定状态 |
| $\beta$ | (13-30Hz) | β节律代表沉浸程度 |
| $\gamma$ | (30Hz以上) | gamma波代表紧张和活跃的高度认知过程 |
伪影干扰
如电力线干扰、肌肉运动(肌电图伪影)、眨眼(眼电图伪影)。 原始脑电信号由于振幅较小,通常会受到各种伪影的污染。
滤波器介绍
目的
为了保持原始信号,滤波器应该有特定的要求。滤波过程的目的是保留信号的特定频率。从干净的脑电图信号中获得的信息可用于临床;如检测癫痫、昏迷、颅脑损伤、脑损伤及脑卒中。
评价指标
均方误差(MSE)
 其中x、y为两个有限长度(离散信号),N为信号样本的个数,xi、yi为x、y中第i个样本的值。
其中x、y为两个有限长度(离散信号),N为信号样本的个数,xi、yi为x、y中第i个样本的值。
峰值噪声比(PSNR)
MSE值通常转换为PSNR值,以分贝值来确定图像的质量。  其中L为允许图像像素强度的动态范围。
其中L为允许图像像素强度的动态范围。
4阶巴特沃斯带通滤波器
频率(带通)选择
截止频率为4 ~ 40 Hz delta频率(低于4hz)被消除了,因为它被认为是噪声,而40hz在分析过程所需的伽马频率范围内,也可以消除电源线干扰(50至60hz)。
流程
流程图注解
选择这些通道是因为它对分析记忆过程很重要。通道分别为Fp1(注意)、Fz(工作记忆)和Pz(认知加工)。 
平稳小波变换滤波器
频率(带通)选择
选择了具有5个分解层次的dB3小波母波 选择该小波母是因为它能够检测和定位脑电信号中的峰值。突波特征包括肌电信号(肌肉运动)、眼电信号(眨眼)。SWT筛选包括三个步骤。
剔除高频噪声采用软阈值法剔除低频噪声重构信号
流程
MSE误差
| 滤波器名称 | Fp1 | Fz | Pz | | – | – | – | – | | Butterworth | 20.42 | 24.50 | 30.50 | | SWT | 2.43 | 2.32 | 2.01 |
// --echarts--
function (chart) {
chart.setOption({
// backgroundColor: '#2c343c',
title: {
text: '滤波器MSE分析',
left: 'center',
top: 0,
textStyle: {
color: '#888'
}
},
legend: {top: 30,},
tooltip : {
trigger: 'axis',
axisPointer: {
type: 'shadow'
}
},
toolbox: {
show: true,
orient: 'vertical',
left: 'right',
top: 'center',
feature: {
mark: { show: true },
dataView: { show: true, readOnly: false },
magicType: { show: true, type: ['line', 'bar', 'stack'] },
restore: { show: true },
saveAsImage: { show: true }
}
},
dataset: {
// 提供一份数据。
source: [
['MSE', 'Butterworth', 'SWT'],
['Fp1', 20.42, 2.43],
['Fz', 24.5, 2.32],
['Pz', 30.5, 2.01],
]
},
xAxis: {type: 'category'},
yAxis: {type: 'value'},
series: [
{
type: 'bar',
emphasis: {
focus: 'series'
},
itemStyle: {
normal: {
label: {
show: true, //开启显示
position: 'top', //在上方显示
textStyle: {
//数值样式
color: 'black',
fontSize: 12,
},
},
},
},
},
{
type: 'bar',
emphasis: {
focus: 'series'
},
itemStyle: {
normal: {
label: {
show: true, //开启显示
position: 'top', //在上方显示
textStyle: {
//数值样式
color: 'black',
fontSize: 12,
},
},
},
},
},
]
}, true)
}
PSNR误差
| 滤波器名称 | Fp1 | Fz | Pz | | – | – | – | – | | Butterworth | 35.07 | 34.27 | 33.32 | | SWT | 44.30 | 44.52 | 54.12 |
// --echarts--
function (chart) {
chart.setOption({
// backgroundColor: '#2c343c',
title: {
text: '滤波器PSNR分析',
left: 'center',
top: 0,
textStyle: {
color: '#888'
}
},
legend: {top: 25,},
tooltip : {
trigger: 'axis',
axisPointer: {
type: 'shadow'
}
},
toolbox: {
show: true,
orient: 'vertical',
left: 'right',
top: 'center',
feature: {
mark: { show: true },
dataView: { show: true, readOnly: false },
magicType: { show: true, type: ['line', 'bar', 'stack'] },
restore: { show: true },
saveAsImage: { show: true }
}
},
dataset: {
// 提供一份数据。
source: [
['MSE', 'Butterworth', 'SWT'],
['Fp1', 35.07, 44.3],
['Fz', 34.27, 44.52],
['Pz', 33.32, 45.12],
]
},
xAxis: {type: 'category'},
yAxis: {type: 'value'},
series: [
{
type: 'bar',
emphasis: {
focus: 'series'
},
itemStyle: {
normal: {
label: {
show: true, //开启显示
position: 'top', //在上方显示
textStyle: {
//数值样式
color: 'black',
fontSize: 12,
},
},
},
},
},
{
type: 'bar',
emphasis: {
focus: 'series'
},
itemStyle: {
normal: {
label: {
show: true, //开启显示
position: 'top', //在上方显示
textStyle: {
//数值样式
color: 'black',
fontSize: 12,
},
},
},
},
},
]
}, true)
}
结论
平稳小波变换在三个通道处的PSNR值要比Butterworth带通滤波器大。 这意味着更多的噪音被过滤掉了。SWT滤波器能够去除肌电图和眼电图的伪影,而Butterworth带通滤波器不能去除所有伪影。与巴特沃斯带通滤波器相比,平稳小波变换去除噪声效果更好。
补充
WT滤波器原理
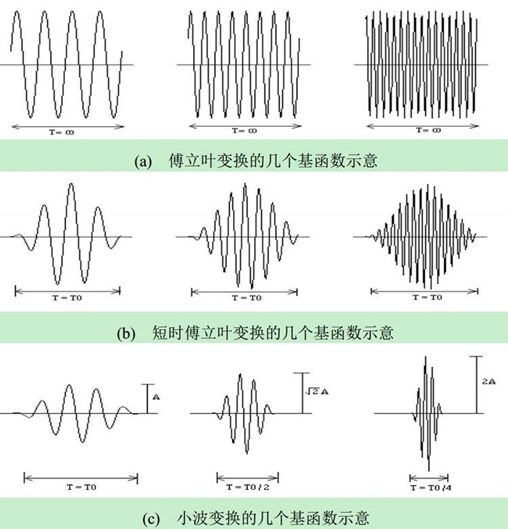
短时傅立叶变换(Short-time Fourier Transform,STFT)
也叫加窗傅立叶变换,顾名思义,就是因为傅立叶变换的时域太长了,所以要弄短一点,这样就有了局部性。
定义:把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。"这就是短时傅里叶变换。时域上分成一段一段做FFT,就知道频率成分随着时间的变化情况了.
基函数
-
FT的基函数,不具有紧支撑性,只能筛选频率,使得FT完全丧失了时间信息,不具有时间分辨率。
-
STFT的基函数,是用窗函数截断的sin,cos,具有了紧支撑性,时域平移等同于分窗,使得STFT既能筛选频率,也能筛选时间。但是STFT基函数是:先确定频率,再与窗函数相乘构成的。因此不同的频率,具有同样的时间和频率分辨率。另外,窗函数的长短也比较难以确定。
-
CWT的基函数,是小波函数,具有紧支撑性,时域平移等同于分窗,使得CWT既能筛选频率,也能筛选时间。小波函数在改变频率的时候,是通过"缩放"实现的,这使得小波函数在改变频率的同时,改变了窗长。因此不同的频率,具有不同的时间和频率分辨率,实现了分辨率动态可调。
窗口时间
- 对于低频信号,为了更好地确定频率,我们希望,时域区间宽一些,即时间不确定度大一些,根据海森堡测不准原理,频率不确定度自然小一些;即低频信号,我们希望:宽窗子,低的时域分辨率,高的频域分辨率。
- 对于高频信号,为了更好地在时域定位,我们希望,时域区间窄一些,即时间不确定度小一些,根据海森堡测不准原理,频率不确定度自然大一些;即高频信号,我们希望:窄窗子,高的时域分辨率,低的频域分辨率。
可能理解这一点最好的方式是举例子。首先,因为我们的变换是对时间和频率的函数(不像傅立叶变换,仅仅是对频率的函数),它是二维的(如果加上幅度则是三维)。 

小波
所以窄窗口时间分辨率高、频率分辨率低,宽窗口时间分辨率低、频率分辨率高。 对于加窗傅立叶变换让人头疼的就是窗口的大小问题,如果我们让窗口的大小可以改变,不就完美了吗?答案是肯定的,小波就是基于这个思路,但是不同的是。STFT是给信号加窗,分段做FFT;而小波变换并没有采用窗的思想,更没有做傅里叶变换。小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率,还可以定位到时间了 
 从公式可以看出,不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)、平移量 τ(translation)。
从公式可以看出,不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)、平移量 τ(translation)。
小波参数
尺度a控制小波函数的伸缩
- a小,相当于挤压,频率提高
- a大相当于拉伸,频率降低
平移量τ控制小波函数的平移。
公式前的系数是为了能量守恒,没有特别目的。 尺度就对应于频率(反比),平移量τ就对应于时间。 
小波过程
小波变换用于去噪的过程分为三个阶段:
- 分解过程:选定一种小波基,对信号进行N层小波分解。
- 选择阈值过程:对分解得到的各层系数选择一个阈值,并对细节系数用软阈值处理。
- 重建过程:将处理后的系数通过小波重建恢复原始信号。
阈值函数


首先小波变换其实生成的是连续值,一维连续信号小波变换生成二维连续值。 而正交小波则可以生成离散值(虽然也可以是连续值,但是由于逆变换只需要一系列离散的值,因此只分析离散的点即可。也就是我们通常用的小波分析)。
连续小波变换(这里特指正交小波的连续小波变换)是通过改变分析窗口的尺度,及时移动窗口,与信号做内积(对时间进行积分)来计算的。
在离散情况下,可以理解为采用不同截止频率的滤波器对信号进行不同尺度的分析。信号通过一系列高通滤波器来分析高频,信号通过一系列低通滤波器来分析低频。

无滤波器 
8-30hz带通滤波器 
小波滤波 db3 level=3 硬阈值  小波滤波 db3 level=5 软阈值2
小波滤波 db3 level=5 软阈值2 
带通滤波器 + 小波滤波 db3 level=3 软阈值1  小波滤波 db3 level=3 软阈值1
小波滤波 db3 level=3 软阈值1 
总结评价
小波可能只存在于paper中,而不在工程中吧。
import mne
import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
from mne.decoding import CSP
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn.model_selection import ShuffleSplit, KFold
from sklearn.model_selection import cross_val_score
import pywt
import math
load_path = "P:/Item/EEG/bci2003/dataset_BCIcomp1.mat"
load_data = sio.loadmat(load_path)
eeg_data = np.array(load_data["x_train"]).T
label = np.array(load_data["y_train"])
bandFreqs = [
{'name': 'Delta', 'fmin': 1, 'fmax': 3},
{'name': 'Theta', 'fmin': 4, 'fmax': 7},
{'name': 'Alpha', 'fmin': 8, 'fmax': 13},
{'name': 'Beta', 'fmin': 14, 'fmax': 31},
{'name': 'Gamma', 'fmin': 31, 'fmax': 40}
]
#sgn函数
def sgn(num):
if(num > 0.0):
return 1.0
elif(num ` 0.0):
return 0.0
else:
return -1.0
def wavelet_noising(new_df):
data = new_df
data = data.T.tolist() # 将np.ndarray()转为列表
w = pywt.Wavelet('dB3')#选择dB3小波基
maxlev = pywt.dwt_max_level(len(data), w.dec_len)
ca3, cd3, cd2, cd1 = pywt.wavedec(data, w, level=3) # 3层小波分解
length1 = len(cd1)
length0 = len(data)
abs_cd1 = np.abs(np.array(cd1))
median_cd1 = np.median(abs_cd1)
sigma = (1.0 / 0.6745) * median_cd1
lamda = sigma * math.sqrt(2.0 * math.log(float(length0 ), math.e))
usecoeffs = []
usecoeffs.append(ca3)
#软阈值方法
for k in range(length1):
if (abs(cd1[k]) >= lamda/np.log2(2)):
cd1[k] = sgn(cd1[k]) * (abs(cd1[k]) - lamda/np.log2(2))
else:
cd1[k] = 0.0
length2 = len(cd2)
for k in range(length2):
if (abs(cd2[k]) >= lamda/np.log2(3)):
cd2[k] = sgn(cd2[k]) * (abs(cd2[k]) - lamda/np.log2(3))
else:
cd2[k] = 0.0
length3 = len(cd3)
for k in range(length3):
if (abs(cd3[k]) >= lamda/np.log2(4)):
cd3[k] = sgn(cd3[k]) * (abs(cd3[k]) - lamda/np.log2(4))
else:
cd3[k] = 0.0
usecoeffs.append(cd3)
usecoeffs.append(cd2)
usecoeffs.append(cd1)
recoeffs = pywt.waverec(usecoeffs, w)#信号重构
return recoeffs
def __CalcWP(data, sfreq, wavelet, maxlevel, band):
# 如果maxlevel太小部分波段分析不到
wp = pywt.WaveletPacket(data=data, wavelet=wavelet, mode='symmetric', maxlevel=maxlevel)
# 频谱由低到高的对应关系,这里需要注意小波变换的频带排列默认并不是顺序排列,所以这里需要使用'freq‘排序。
freqTree = [node.path for node in wp.get_level(maxlevel, 'freq')]
# 计算maxlevel最小频段的带宽,采样频率的一半
freqBand = (sfreq/2) / (2 ** maxlevel)
bandResult = []
#######################根据实际情况计算频谱对应关系,这里要注意系数的顺序
for iter_freq in band:
# 构造空的小波包
new_wp = pywt.WaveletPacket(data=None, wavelet=wavelet, mode='symmetric', maxlevel=maxlevel)
for i in range(len(freqTree)):
# 第i个频段的最小频率
bandMin = i * freqBand
# 第i个频段的最大频率
bandMax = bandMin + freqBand
# 判断第i个频段是否在要分析的范围内
if (iter_freq['fmin'] <= bandMin and iter_freq['fmax'] >= bandMax):
# 给新构造的小波包参数赋值
# print('freq',bandMin, bandMax,'fmin',iter_freq['fmin'],'fmax',iter_freq['fmax'])
new_wp[freqTree[i]] = wp[freqTree[i]].data
# 计算对应频率的数据
bandResult.append(new_wp.reconstruct(update=True))
return bandResult
########################################小波包变换-重构造分析不同频段的特征(注意maxlevel,如果太小可能会导致部分频段分析不到)#########################
# 定义WP函数
# epochsData:epochs的数据(mumpy格式)
# sfreq:采样频率
# wavelet:小波类型
# maxlevel:小波层数
# band:频带类型
def WP(epochsData, sfreq, wavelet='db3', maxlevel=8, band=bandFreqs):
# 输出的维度顺序为 频率->epoch->channel->timeData
result = []
for epochData in epochsData:
channel = []
for channelData in epochData:
# print('channel:')
channel.append(__CalcWP(channelData, sfreq, wavelet=wavelet, maxlevel=maxlevel, band=band))
result.append(channel)
return np.array(result).transpose((2, 0, 1, 3))
'''
构建一个Raw对象时,需要准备两种数据,一种是data数据,一种是Info数据,
data数据是一个二维数据,形状为(n_channels,n_times)
'''
ch_names = ['C3','Cz','C4'] # 通道名称
ch_types = ['eeg', 'eeg', 'eeg'] # 通道类型
sfreq = 128 # 采样率
info = mne.create_info(ch_names, sfreq, ch_types) # 创建信号的信息
info.set_montage('standard_1020')
raw_0 = eeg_data[0, :, :]
for i in range(1, 140):
raw_i = eeg_data[i, :, :]
raw_0 = np.concatenate((raw_0, raw_i), axis=1)
raw_data = raw_0
#raw_data = wavelet_noising(raw_data)
raw_data[0] = wavelet_noising(raw_data[0])
raw_data[1] = wavelet_noising(raw_data[1])
raw_data[2] = wavelet_noising(raw_data[2])
# print(raw_data.shape)
# >>>(3, 161280)
raw = mne.io.RawArray(raw_data, info)
# print(raw)
# raw.plot(scalings={'eeg': 'auto'})
# print('数据集的形状为:',raw.get_data().shape)
# print('通道数为:',raw.info.get('nchan'))
# FIR带通滤波
#raw.filter(8., 30., fir_design='firwin', skip_by_annotation='edge')
'''
在创建Epochs对象时,必须提供一个"events"数组,
事件(event)描述的是某一种波形(症状)的起始点,其为一个三元组,形状为(n_events,3):
第一列元素以整数来描述的事件起始采样点;
第二列元素对应的是当前事件来源的刺激通道(stimulus channel)的先前值(previous value),该值大多数情况是0;
第三列元素表示的是该event的id.
'''
# 创建 events & event_id
events = np.zeros((140, 3), dtype='int')
k = sfreq * 3
for i in range(140):
events[i, 0] = k
k += sfreq * 9
events[i, 2] = label[i]
# print(events)
event_id = dict(left_hand=1, right_hand=2)
# 创建epochs
tmin, tmax = -1., 4. # 记录点的前1秒后4秒用于生成epoch数据
epochs = mne.Epochs(raw, events, event_id
, tmin, tmax
, proj=True
, baseline=(None, 0)
, preload=True)
# 想要分析的目标频带
#bandIndex = 4
firFilter = epochs.copy().filter(bandFreqs[1]['fmin'], bandFreqs[4]['fmin'])
# 计算小波包滤波后的数据并绘图
wpFilter = WP(epochs.get_data(), sfreq)
epochs.selection = wpFilter
#获取小波分解的最大层级
maxlev = pywt.swt_max_level(len(epochs.get_data()))
coeffs= pywt.swt(epochs.selection,'db3', level = maxlev) # 将信号进行小波分解
coeffs[0][0].fill(0)
coeffs[maxlev-1][1].fill(0)
datarec = pywt.iswt(coeffs,'db3') # 将信号进行小波重构
###使用滤波器
#epochs = firFilter
#epochs.selection = datarec
epochs_train = epochs.copy().crop(tmin=1., tmax=2.) # 截取其中的1秒到2秒之间的数据,也就是提示音后
# 1秒到2秒之间的数据(这个在后面滑动窗口验证的时候有用)
labels = epochs.events[:, -1]
# print(labels)
#特征提取和分类
scores = []
epochs_data = epochs.get_data() #获取epochs的所有数据,主要用于后面的滑动窗口验证
#print(epochs_data.shape)
#>>>(140, 3, 641)
epochs_data_train = epochs_train.get_data() #获取训练数据
#print(epochs_data_train.shape)
#>>>(140, 3, 129) #也是多了一个
kf = KFold(n_splits=5 #交叉验证模型的参数
, shuffle=True
, random_state=42)
cv_split = kf.split(epochs_data_train) #输出索引以将数据分为训练集和测试集
svm = SVC() #支持向量机分类器
csp = CSP(n_components=2 #2个分量的CSP
,reg=None
,log=False
,norm_trace=False)
clf = Pipeline([('CSP', csp), ('SVM', svm)]) #创建机器学习的Pipeline
scores = cross_val_score(clf #获取交叉验证模型的得分
, epochs_data_train
, labels
, cv=kf
, n_jobs=-1)
class_balance = np.mean(labels ` labels[0]) #输出结果,准确率和不同样本的占比
class_balance = max(class_balance, 1. - class_balance)
print("Classification accuracy: %f / Chance level: %f" % (np.mean(scores)
, class_balance))
csp.fit_transform(epochs_data, labels)
csp.plot_patterns(epochs.info #绘制CSP不同分量的模式图
, ch_type='eeg'
, units='Patterns (AU)'
, size=1.5)
# 验证算法的性能
w_length = int(sfreq * 1.5) # 设置滑动窗口的长度
w_step = int(sfreq * 0.1) # 设置滑动步长
w_start = np.arange(0, epochs_data.shape[2] - w_length, w_step)
# 每次滑动窗口的起始点
scores_windows = [] # 得分列表用于保存模型得分
# 交叉验证计算模型的性能
for train_idx, test_idx in cv_split:
y_train, y_test = labels[train_idx], labels[test_idx] # 获取测试集和训练集数据
X_train = csp.fit_transform(epochs_data_train[train_idx], y_train) # 设置csp模型的参数,提取相关特征,用于后面的svm分类
svm.fit(X_train, y_train) # 拟合svm模型
score_this_window = [] # 用于记录本次交叉验证的得分
for n in w_start:
X_test = csp.transform(epochs_data[test_idx][:, :, n:(n + w_length)]) # csp提取测试数据相关特征
score_this_window.append(svm.score(X_test, y_test)) # 获取测试数据得分
scores_windows.append(score_this_window) # 添加到总得分列表
w_times = (w_start + w_length / 2.) / sfreq + epochs.tmin # 设置绘图的时间轴,时间轴上的标志点为窗口的中间位置
# 绘制模型分类结果的性能图
plt.figure()
plt.plot(w_times, np.mean(scores_windows, 0), label='Score')
plt.axvline(0, linestyle='--', color='k', label='Onset')
plt.axhline(0.5, linestyle='-', color='k', label='Chance')
plt.xlabel('time (s)')
plt.ylabel('classification accuracy')
plt.title('Classification score over time')
plt.legend(loc='lower right')
plt.show()
source: test_long/folder1/1.SWT与Butterworth比较.md