土壤湿度变化因素分析及预测模型

草原土壤湿度变化是在时空尺度上的变化。检测土壤湿度对掌握作物对水的需要情况，对指导农业生产有至关重要的意义。影响土壤湿度的因素往往分为以下几类:

  • 植被状况
  • 人为活动
  • 气象因素
  • 土壤特征

这些都可能影响土壤含水量变化。寻找、求证土壤湿度变化的影响因素，对土壤湿度变化模型的构建及未来土壤湿度的预测可以提供重要的理论支持。基于此目的，本章尝试对土壤湿度数据进行分析，从机理和数理统计两方面角度，寻找并求证影响土壤湿度变化的影响因素及其相关性程度。在此基础上尝试构建土壤湿度变化模型，并对未来两年的土壤湿度变化作出预测。

问题二的分析与思路

本题的要求是根据土壤湿度变化的影响因素（包括土壤蒸发量、 植被指数、气温、平均露点温度、 降水量，风速等要素）进行分析，建立相关土壤湿度模型，并对未来两年的土壤湿度变化进行预测。

为了了解锡林郭勒草原的土壤湿度变化，本文试图调查和综合当前关于土壤湿度模型层次结构的一些思想，给出了一些关于预测模型的正式描述，并调查了预测模型用于生成，测试和确认假设的可行方式，结合了土壤湿度模型的一些特点，用于预测实际过程中的土壤湿度变化问题。

本题的解决思路是基于历年草原监测站收集的数据，分析其特征和变化规律，着重于土壤湿度对时间的倾向率、土壤湿度变化的平稳性与周期性。探讨影响土壤湿度变化的多种可能因素，比如土壤蒸发量、植被指数、气温、平均露点温度、 降水量，风速等等。收集并整理上述因素对土壤湿度变化影响的数据，进行数据预处理，分析这些因素的影响程度。然后建立多因素的多元回归土壤湿度变化预测模型，设定好参数之后将模型应用于实际问题，检验模型的正确性。最后利用基于SARIMA以及GRU神经网络的两种预测模型，对比效果后, 选择更优的方法对未来两年土壤湿度进行预测。 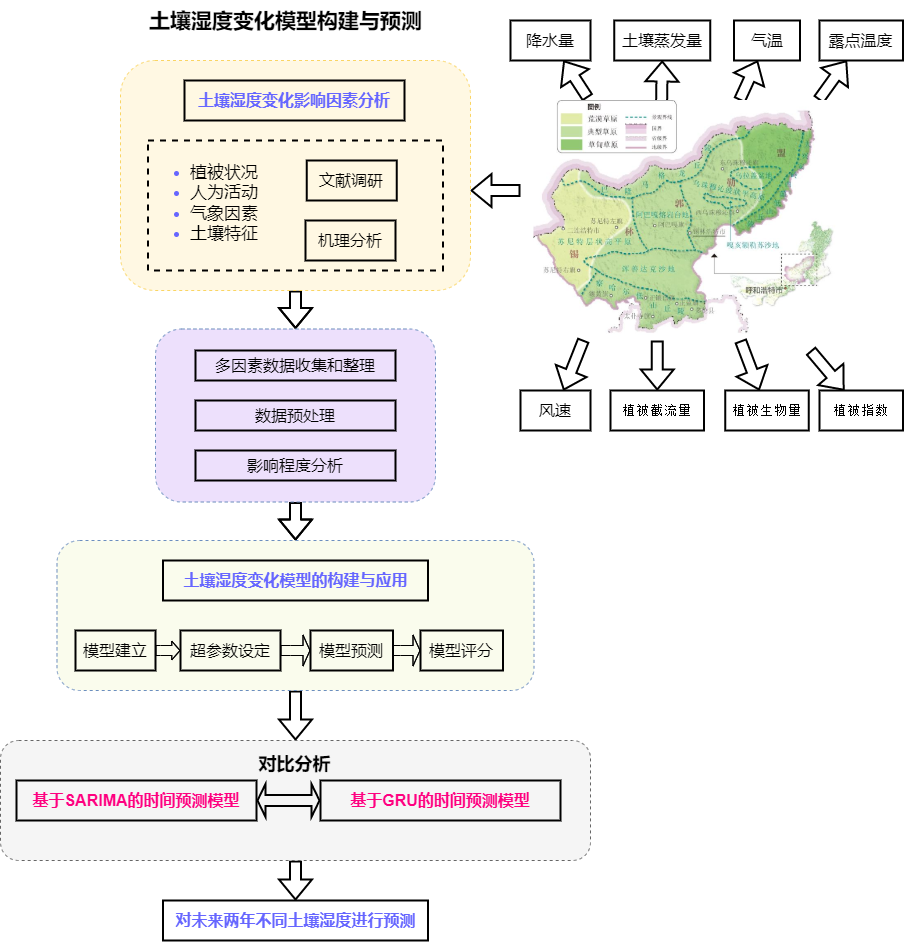Img

数据可视化

农田水分在土壤—作物—大气连续体内‚通过降水、入渗、蒸发、蒸腾等形式周而复始地循环‚其过程十分复杂。需要探究各个检测量之间的内在机理.

土壤蒸发量

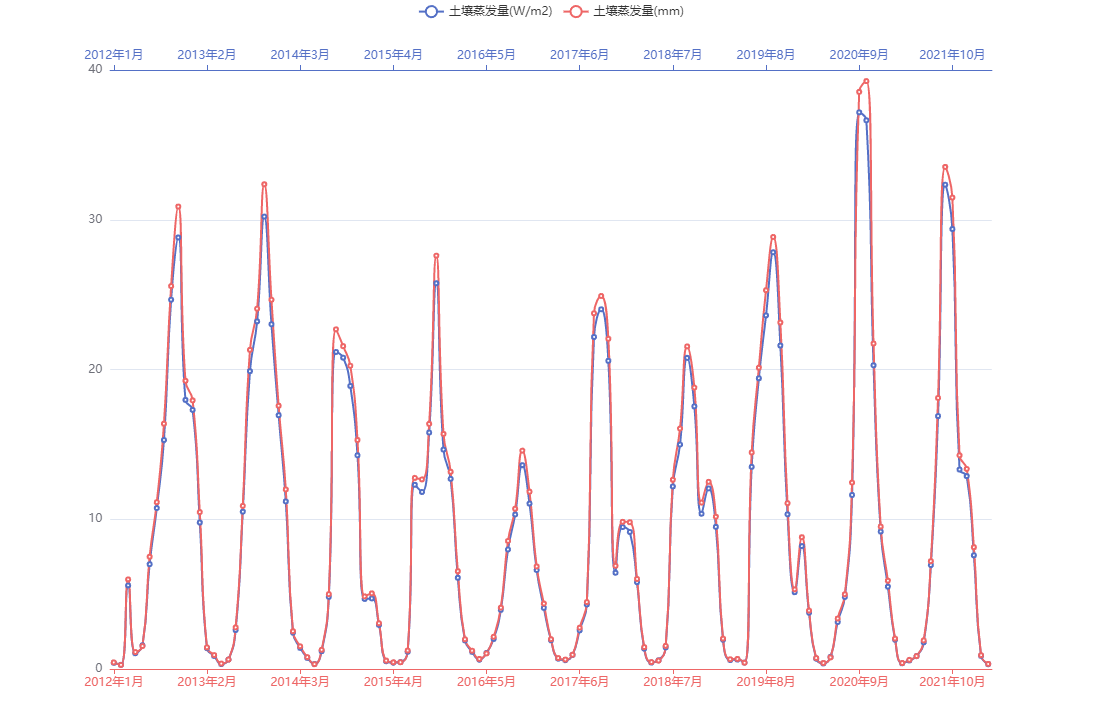
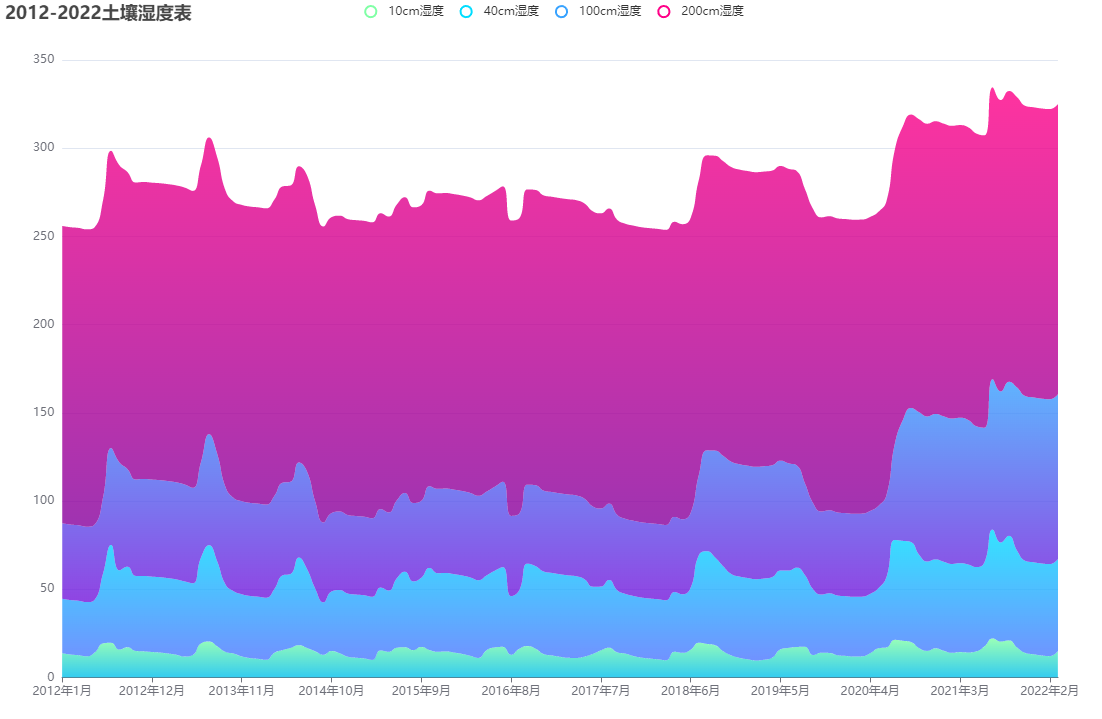
将2012年至2022年的土壤蒸发量进行可视化, 如下图所示. Img

土壤湿度

Img

降水量、叶面积指数、植被指数

将2012年至2022年的降水量、叶面积指数、植被指数进行可视化, 如下图所示. 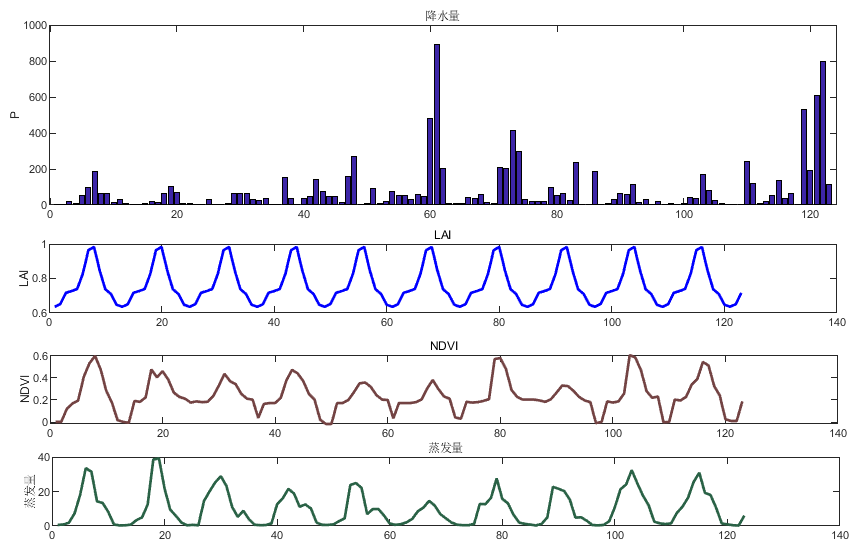Img

数据预处理

数据缺失值的处理

由于数据记录部门及周期不同，不同数据集的数据量不尽相同，为了使各变量的数据集具有可用性，对数据集中的缺失值做相应处理。本文对这些数据集中的缺失值处理方法主要包括以下三种：

  • 删除缺失值
    • 对汇总的数据进行缺失值判断,容易得出积雪深度,平均最大瞬时风速,最大瞬时风速极值这些数值有缺失,且这些数据经过机理分析对分析问题影响不大,所以可以删去.
  • 均值插补
    • 采用序列的均值来替换缺失值。
  • 基于序列趋势的插值
    • 对于序列中间的缺失值，如一段历史数据中某几个年份缺乏记录，首先分析该序列的趋势，用最佳的回归模型进行拟合或者采用时间序列模型进行拟合，从而计算出相应的估计值，替换缺失值。
    • 对于序列末尾的缺失值，可以通过对序列趋势及特性的分析，采用回归模型或时间序列模型来拟合预测，得到对应的预测值以替换缺失值。对于序列首段的缺失值，可将序列先倒序后再采用前述进行逆时间预测，得到对应的预测值从而替换缺失值。

数据去极值、标准化与平稳性检验

去极值就是排除一些极端值的干扰,在做回归分析的时候，因为过大或过小的数据可能会影响到分析结果，离群值会严重影响因子和收益率之间的相关性估计结果，因此需要对那些离群值进行处理。而由于各变量的单位和数量级并不相同，为了便于构建多变量回归模型，在去极值后可将各变量的数据进行标准化。

3σ法去极值

3σ法源于最经典的统计学3σ原则，即正态分布的数分布在（μ-3σ,μ+3σ)中的概率为99.73%，在3σ外的概率是0.27%，其中μ代表平均值，σ是标准差，3σ去极值法其实就是把离平均值太远的值算作极端值，距离超过3倍标准差以上的就是远。

graph LR A(确定上下限) -->B(找出超限值数据) B --> C(将离群值改为限幅值)

z-score 标准化

标准分数（standard score）也叫 z分数（z-score），是将变量值与平均数的差再除以标准差的过程。在变量的原始值低于平均值时 Z 值为负数，反之则为正数。 本文应用Z-score归一化来预处理数据添加随机噪声以防止过度拟合，如以下公式所示： \(\mathrm{X}^{*}=\frac{\mathrm{X}-\mu}{\delta}+\alpha \mathrm{N}\)

符号 含义
$X$ 表示原始数据
$X^{*}$ 表示预处理后的数据
μ 表示数据的平均值
δ 表示标准偏差
N 表示随机噪声
α 控制随机噪声的百分比

ADF检验

在使用很多时间序列模型的时候，如 ARMA、ARIMA，都会要求时间序列是平稳的，所以一般在研究一段时间序列的时候，第一步都需要进行平稳性检验，除了用肉眼检测的方法，另外比较常用的严格的统计检验方法就是ADF检验，也叫做单位根检验。

简单点来说, ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。所以，ADF检验的 H0 假设就是存在单位根，如果得到的显著性检验统计量小于三个置信度（10%，5%，1%），则对应有（90%，95，99%）的把握来拒绝原假设。

GRU网络模型预测

GRU（Gate Recurrent Unit）是循环神经网络（Recurrent Neural Network, RNN）的一种。和LSTM（Long-Short Term Memory）一样，也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。相比LSTM，使用GRU能够达到相当的效果，并且相比之下更容易进行训练，能够很大程度上提高训练效率，因此很多时候会更倾向于使用GRU。

GRU的基本结构

GRU的输入输出结构与普通的RNN是一样的, 其中的内部思想与LSTM相似。有一个当前的输入$x^t$，和上一个节点传递下来的隐状态$h^{t-1}$，这个隐状态包含了之前节点的相关信息。结合$x^t$和$h^{t-1}$，GRU会得到当前隐藏节点的输出$y^t$和传递给下一个节点的隐状态$h^{t}$。 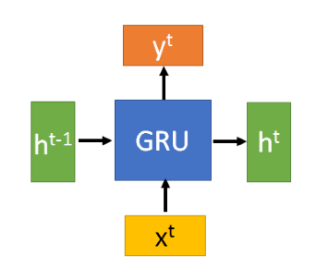Img

GRU的内部结构

首先，我们先通过上一个传输下来的状态$h^{t-1}$和当前节点的输入$x^t$来获取两个门控状态。如下图所示，其中$r$控制重置的门控（reset gate），$z$为控制更新的门控（update gate） Img 得到门控信号之后，首先使用重置门控来得到"重置"之后的数据$h^{t-1'}$，再将$h^{t-1'}$与输入$x^t$进行拼接，再通过一个tanh激活函数来将数据放缩到-1~1的范围内。即得到如下图所示的$h^{‘}$。 Img 这里的$h^{‘}$主要是包含了当前输入的$x^t$数据。有针对性地对$h^{‘}$添加到当前的隐藏状态，相当于"记忆了当前时刻的状态"。

GRU整体网络模型结构

Img

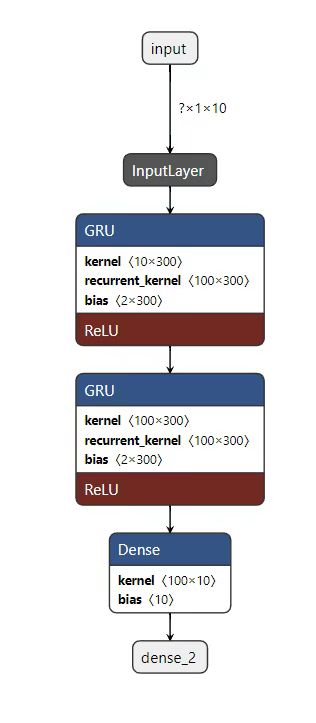
GRU算法三线表

训练模型

训练轮次epoch=300 , adam优化器, MSE损失函数, RELU激活函数

训练结果

Img

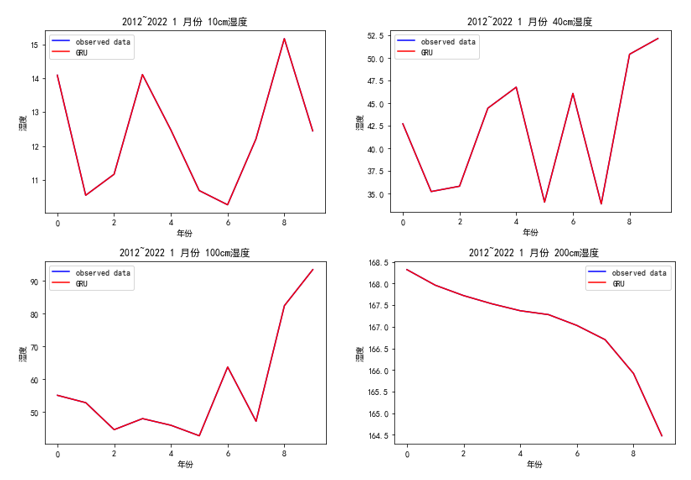
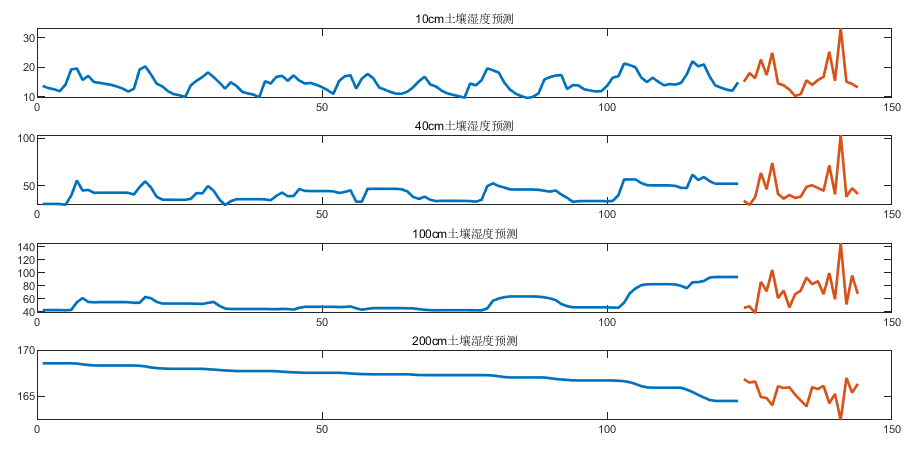
预测结果

Img

评价模型

原理

平均绝对误差MAE ( mean absolute error )是绝对误差的平均值，它其实是更一般形式的误差平均值。 因为如果误差是[-1,0,1].平均值就是0,但这并不意味之系统不存在误差，只是正负相互抵消了，因此我们要加上绝对值。它的定义表达式 \(\mathrm{MAE}=\frac{\sum_{i=1}^{n}\left|y_{i}-x_{i}\right|}{n}\) 换成更直接的表达式:

\(M A E=\frac{1}{n} \sum_{k=1}^{n} \mid\left(\right. actual _{1}- predicted \left._{1}\right)|+\cdots+|\left(\right. actual _{n}- predicted \left._{n}\right) \mid\) 而均方根误差RMSE ( root mean squared error ),也有资料称为RMSD，也可以测量误差的平均大小，它是预测值和实际观测之间平方差异平均值的平方根。他的定义为:

\(\mathrm{RMSD}=\sqrt{\frac{\sum_{t=1}^{T}\left(\hat{y}_{t}-y_{t}\right)^{2}}{T}}\) 换成更直接的表达式: \(R M S E=\sqrt{\frac{\sum_{k=1}^{n}\left(\text { actual }_{1}-\text { predicted }_{1}\right)^{2}+\cdots+\left(\text { actual }_{n}-\text { predicted }_{n}\right)^{2}}{n}}\)

评价总结

| 土壤深度 | RMSE | MAE | | – | – | – | | 一月10cm土壤湿度 | 0.00016791602 | 0.00014801025 | | 一月40cm土壤湿度 | 0.0014447744 | 0.0011886597 | | 一月100cm土壤湿度 | 0.0051352843 | 0.0040065767 | | 一月200cm土壤湿度 | 0.00016791602 | 0.00014801025 |

存在过拟合现象, 预测效果不佳, 推测是由于训练轮次太多, 每层配置的GRUCell过多.

SARIMA模型预测

1.通过ARIMA时间序列预测降水量、蒸发量、NDVI等，需要注意季节性，使用季节性时间序列预测（SARIMA，见代码），使用时间序列预测前需要使用平稳性检验。检验方法有很多种，包括ADF、KPSS、P-P等。这里用ADF检验和KPSS检验。 另外，Durbin-Watson 统计是计量经济学分析中最常用的自相关度量。该值接近2，则可以认为序列不存在一阶相关性。（详见代码） 2.LAI是周期函数，计算未来月份的LAI，进一步计算未来月份的ICmax 3.计算未来月份的ICstore(t) 4.根据未来月份的ICstore(t)和预测的降水量和蒸发量，推导含水量变化 通过含水量变化推导湿度变化

模型原理

ARIMA模型(Autoregressive Integrated Moving Average model)，差分整合移动平均自回归模型，又称整合移动平均自回归模型，时间序列预测分析方法之一。ARIMA(p,d,q)中，AR是"自回归"，p为自回归项数;MA为"滑动平均"，q为滑动平均项数，d为使之成为平稳序列所做的差分次数(阶数)。 \(A R I M A(p, d, q)\left\{\begin{array}{l}A R(p)-p阶自回归 \\ M A(q)-q阶滑动平均 \\ d \text { 为使之成平稳序列的差分次数 }\end{array}\right.\)

AR模型

自回归只适用于预测与自身前期相关的现象，数学模型表达式如下： \(y_{t}=\mu+\sum_{i=1}^{p} r_{i} y_{t-i}+\epsilon_{t}\)

符号 含义
$y_{t}$ 当前值，是常数项
$p$ 阶数
$r_i$ 自相关系数
$\epsilon _{t}$ 误差, 符合正态分布

该模型反映了在t时刻的目标值值与前t-1~p个目标值之前存在着一个线性关系，即： \(y_{t} \sim r_{1} y_{t-1}+r_{2} y_{t-2}+\ldots+r_{p} y_{t-p}\)

MA模型

移动平均模型关注的是自回归模型中的误差项的累加，数学模型表达式如下： \(y_{t}=\mu+\epsilon_{t}+\sum_{i=1}^{q} \theta_{i} \epsilon_{t-i}\) 该模型反映了在t时刻的目标值值与前t-1~p个误差值之前存在着一个线性关系，即： \(y_{t} \sim \theta_{1} \varepsilon_{t-1}+\theta_{2} \varepsilon_{t-2}+\ldots+\theta_{p} \varepsilon_{t-p}\)

ARMA模型

该模型描述的是自回归与移动平均的结合，具体数学模型如下： \(Y_{t}=\beta_{0}+\beta_{1} Y_{t-1}+\beta_{2} Y_{t-2}+\cdots+\beta_{p} Y_{t-p}+\epsilon_{t}+\alpha_{1} \epsilon_{t-1}+\alpha_{2} \epsilon_{t-2}+\cdots+\alpha_{q} \epsilon_{t-q}\)

ARIMA模型

基本原理：将数据通过差分转化为平稳数据，再将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。

SARIMA模型

季节性整合自回归移动平均模型，将季节差分与ARIMA模型相结合的SARIMA模型用于具有周期性特征的时间序列数据建模。应用于包含趋势和季节性的单变量数据，SARIMA由趋势和季节要素组成的序列构成。 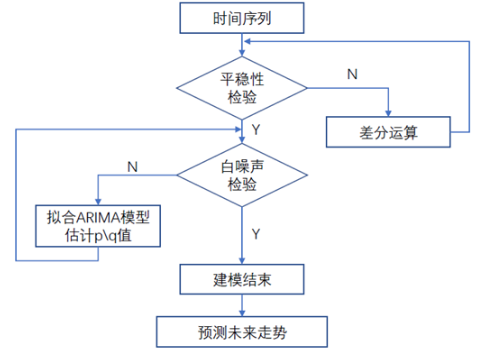Img

模型建模步骤

  1. 观察时间序列的周期，确定周期长度S；
  2. 通过非季节差分和周期为x的季节差分保证时间序列的平稳性，确定d值；
  3. 通过ACF和PACF确定非季节性模型p、q值；
  4. 通过季节分解的序列图、ACF和PACF确定季节模型的P、D、Q值；
  5. 将选定的pdq和PDQ的可能值代入SARIMA模型；
  6. 根据AIC最小值和Q检验来选取最优模型。

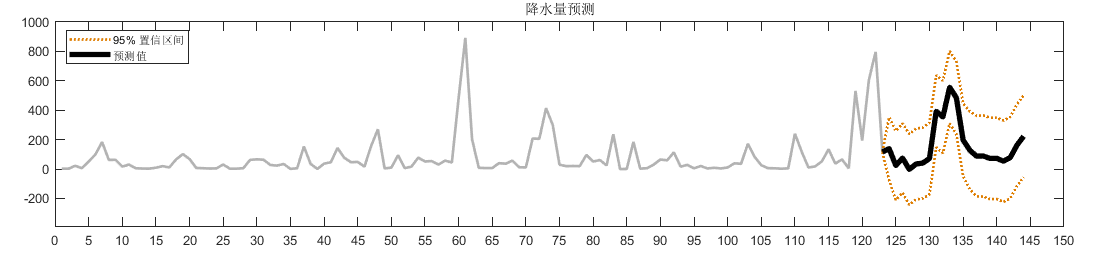
降水量预测

Img

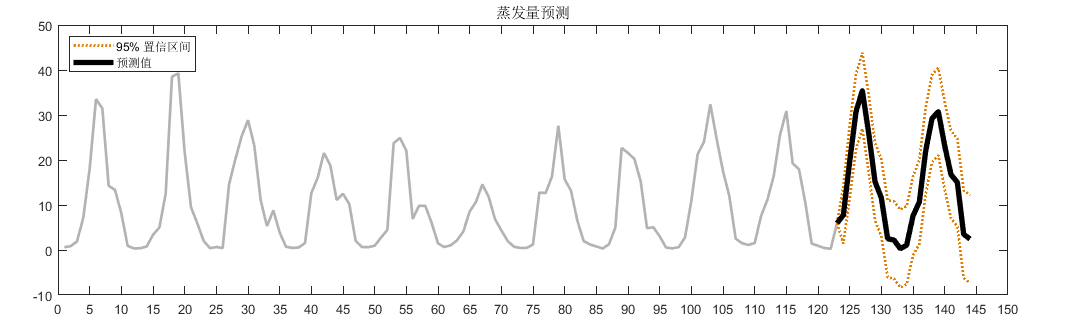
蒸发量预测

Img

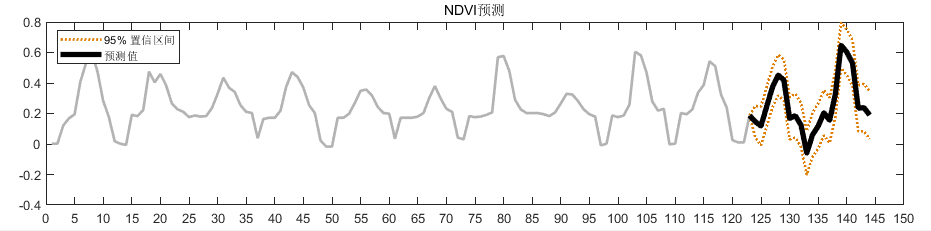
NDVI预测

Img

土壤湿度预测

Img

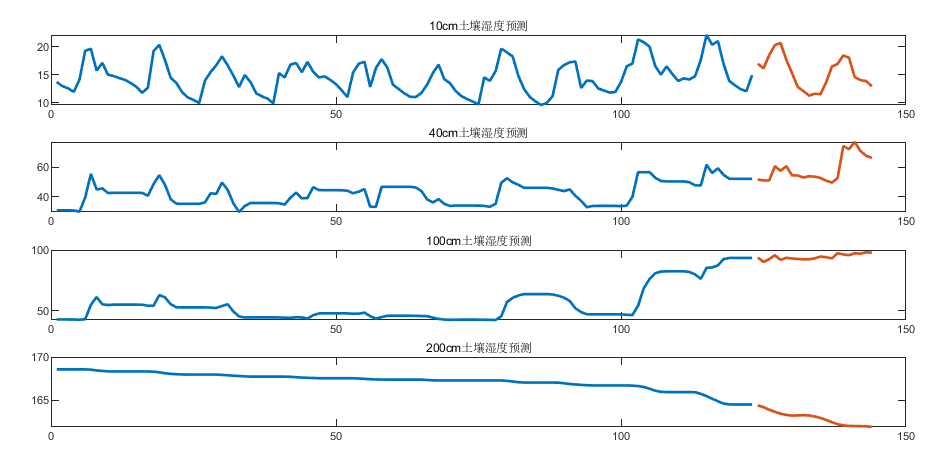
DW检验

德宾-沃森检验,简称D-W检验，是目前检验自相关性最常用的方法，但它只适用于检验一阶自相关性。引入自相关回归系数ρ，当ρ=0表示无自相关性，ρ>0表示存在正自相关性,ρ<0表示存在负自相关性. 因为自相关系数ρ的值介于-1和1之间，所以 0≤DW≤４。 \(D W=\frac{\sum_{t=2}^{n}\left(e_{t}-e_{t-1}\right)^{2}}{\sum_{t=2}^{n} e_{t}^{2}} \underset{n \text { 较大 }}{\approx} 2\left[1-\frac{\sum_{t=2}^{n} e_{t} e_{t-1}}{\sum_{t=2}^{n} e_{t}^{2}}\right] = 2(1- \hat{\rho})\) \(\hat{\rho}=\sum_{t=2}^{n} e_{t} e_{t-1} / \sum_{t=2}^{n} e_{t}^{2}\)

参数 含义
$DW＝0 < = > ρ＝1$ 存在正自相关性
$DW＝４ < = > ρ＝-1$ 存在负自相关性
$DW＝２ < = > ρ＝0$ 不存在（一阶）自相关性
预测对象 DW检验值
降水量 1.9840
蒸发量 2.0067
NDVI 2.0774

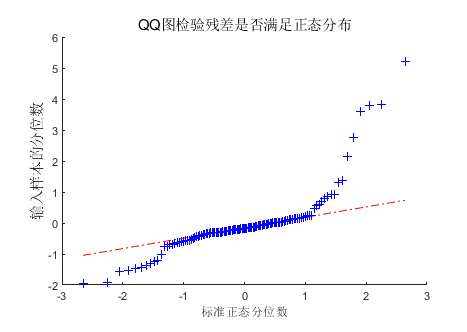
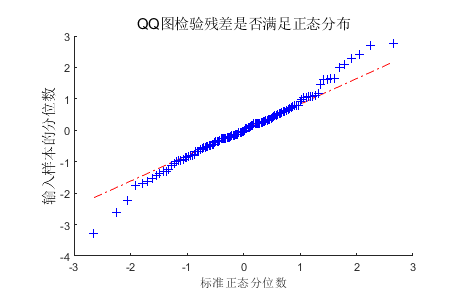
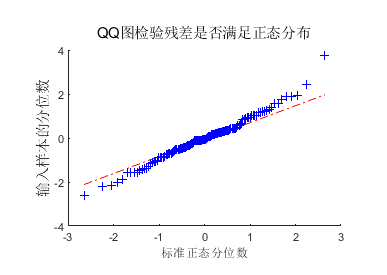
QQ plot图

QQ plot图的全称是Quantile-Quantile Plot，即分位数-分位数图。它们本质上就是做两组数据的比较，判断它们是否基本一致。

以样本重复性散点图为例，如果某个基因的表达量在样本C1和C2两个生物学重复中相同或相近，那么这个基因在这个散点图中X和Y轴坐标应该是相同或相近的，即这个点应该位于这个图形的45°对角线上。

如果大部分点位于对角线上，说明这两组值基本一致，即两个样本的重复性良好。

降水量

Img

蒸发量

Img

NDVI

Img

评价

在散点图的左下角是显著性低的位点，即确定与性状不关联的位点，这些位点的P value观测值应该与期望值一致。而图中这些点的确位于对角线上，说明分析模型是合理的。而在图形的右上角则是显著性较高的位点，是潜在与性状相关的候选位点。这些点位于对角线的上方，即位点的P value观测值超过了期望值，说明这些位点的效应超过了随机效应，进而说明这些位点是与性状显著相关的。

总结

SARIMA的结果优于GRU, 故本文对于第二题选择的方法为SARIMA 填表如下: 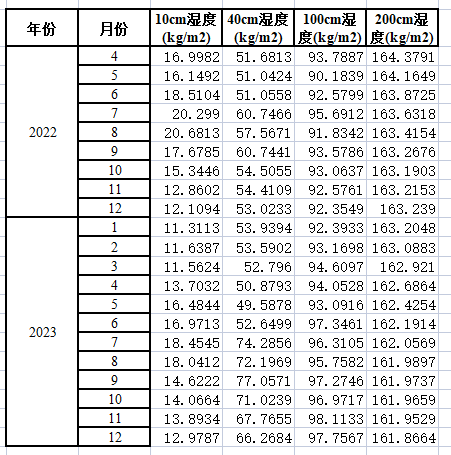Img 由D-W值的大小确定自相关性：